
题目列表(包括答案和解析)
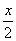
hn=![]() 容易知道x6=1.
容易知道x6=1.
观察上图,不难发现,正2n边形的面积等于正n边形的面积加上n个等腰三角形的面积,即S2n=Sn+n·![]() ·xn(1-hn)(n≥6)利用这个递推公式,我们可以得到:
·xn(1-hn)(n≥6)利用这个递推公式,我们可以得到:
正六边形的面积S6=6×![]() ;正十二边形的面积S12=_______________;正二十四边形的面积S24=_______________________.
;正十二边形的面积S12=_______________;正二十四边形的面积S24=_______________________.
……
当n不断增大,S2n的值不断趋近于什么?
用循环结构编写程序.
| PnPn+1 |
| 1 |
| 3 |
| Pn-1Pn |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com