
题目列表(包括答案和解析)
(2012年高考江西卷理科20) (本题满分13分)
已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足![]() .
.
(1) 求曲线C的方程;
(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l向:是否存在定点P(0,t)(t<0),使得l与PA,PB都不相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值。若不存在,说明理由。
(本题满分13分)已知等差数列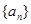 的公差
的公差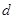 大于0,且
大于0,且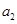 、
、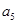 是方程
是方程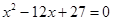 的两根.数列
的两根.数列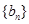 的前
的前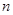 项和为
项和为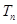 ,满足
,满足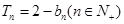
(Ⅰ)求数列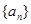 ,
,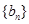 的通项公式;
的通项公式;
(Ⅱ)设数列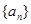 的前
的前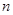 项和为
项和为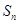 ,记
,记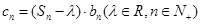 .若
.若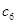 为数列
为数列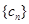 中的最大项,求实数
中的最大项,求实数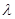 的取值范围.
的取值范围.
(本题满分13分)
已知点 和互不相同的点
和互不相同的点 ,
,
满足 ,其中
,其中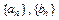 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。
(1)求 的值;
的值;
(2)证明 的公差为d =0,或
的公差为d =0,或 的公比为q=1,点
的公比为q=1,点 在同一直线上;
在同一直线上;
(3)若d  0,且q
0,且q  1,点
1,点 能否在同一直线上?证明你的结论
能否在同一直线上?证明你的结论
(本题满分13分)
已知等差数列![]() 的公差大于0,且
的公差大于0,且![]() 是方程
是方程![]() 的两根,数列
的两根,数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
(本题满分13分)
已知等差数列![]() 的公差大于0,且
的公差大于0,且![]() 是方程
是方程![]() 的两根,数列
的两根,数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
命题人:阳志长(株洲县五中) 方厚良(株洲县五中) 邓秋和(株洲市二中)
审题人:邓秋和(株洲市二中) 阳志长(株洲县五中) 方厚良(株洲县五中)
一、选择题:(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
A
D
A
A
D
B
B
二、填空题:(本大题共5小题,每小题5分,共25分。把答案填写在相应的横线上。)
11. 2 12.数学文科.files/image219.gif) 13.20
13.20数学文科.files/image221.gif) 14.-3或-7 15.
14.-3或-7 15.数学文科.files/image223.gif)
三、解答题:(本大题共6小题,满分75分,解答要写出文字说明、证明过程或演算步骤)
16.解:(Ⅰ)根据正弦定理,由数学文科.files/image225.gif) 得
得数学文科.files/image227.gif) ,----2分
,----2分
∴锐角数学文科.files/image229.gif) 。???4分
。???4分
(Ⅱ)∵数学文科.files/image231.gif) ,
,数学文科.files/image229.gif)
数学文科.files/image233.gif) ,???5分
,???5分
数学文科.files/image235.gif)
数学文科.files/image123.gif) =
=数学文科.files/image237.gif)
=数学文科.files/image239.gif) 。???9分
。???9分
数学文科.files/image241.gif) ,
,数学文科.files/image243.gif) -----10分
-----10分
数学文科.files/image245.gif) ,
,数学文科.files/image247.gif) ,
,
故数学文科.files/image123.gif) 的取值范围是
的取值范围是数学文科.files/image249.gif) 。-----12分
。-----12分
17.解:(Ⅰ)记A表示事件:进入该健身中心的1位健身者选择的是甲种项目,B表示事件:进入该健身中心的1位健身者选择的是乙种项目,则事件A与事件B相互独立,P(A)=数学文科.files/image125.gif) ,P(B)=
,P(B)=数学文科.files/image127.gif) 。???-1分
。???-1分
故进入该健身中心的1位健身者选择甲、乙两种项目中的一项的概率为:P数学文科.files/image253.gif) =
=数学文科.files/image255.gif) =P(A)
=P(A)数学文科.files/image257.gif) +
+数学文科.files/image259.gif) =
=数学文科.files/image261.gif) 。-??4分
。-??4分
(Ⅱ)记C表示事件:进入该健身中心的1位健身者既未选择甲种又未选择乙种健身项目,D表示事件:进入该健身中心的4位健身者中,至少有2位既未选择甲种又未选择乙种健身项目,A2表示事件:进入该健身中心的4位健身者中恰有2位既未选择甲种又未选择乙种健身项目,A3表示事件:进入该健身中心的4位健身者中恰有3位既未选择甲种又未选择乙种健身项目,A4表示事件:进入该健身中心的4位健身者中恰有4位既未选择甲种又未选择乙种健身项目,???5分
则P(C)=数学文科.files/image263.gif) ,???7分
,???7分
数学文科.files/image265.gif) ,???8分
,???8分
数学文科.files/image267.gif) ,???9分
,???9分
数学文科.files/image269.gif) ???10分
???10分
数学文科.files/image271.gif) 。???12分
。???12分
18.解:(Ⅰ)
数学文科.files/image273.gif) ,
,
数学文科.files/image275.gif) 。???3分
。???3分
数学文科.files/image276.gif) (Ⅱ)如图,以A为原点,DA、AB、AP所在直线为
(Ⅱ)如图,以A为原点,DA、AB、AP所在直线为数学文科.files/image278.gif) 、
、数学文科.files/image280.gif) 、
、数学文科.files/image282.gif) 轴,建立空间直角坐标系
轴,建立空间直角坐标系数学文科.files/image284.gif) ,则B
,则B数学文科.files/image286.gif) ,C(-2,4,0),P(0,0,2)。???5分
,C(-2,4,0),P(0,0,2)。???5分
设平面PBC的一个法向量数学文科.files/image288.gif)
由数学文科.files/image290.gif)
取数学文科.files/image292.gif) 得,
得, 数学文科.files/image294.gif) ,
,数学文科.files/image296.gif) ,???7分
,???7分
故点A到平面PBC的距离数学文科.files/image298.gif) ???9分
???9分
(Ⅲ)设平面PDC的一个法向量数学文科.files/image300.gif) 由
由
数学文科.files/image302.gif) ,
,
取数学文科.files/image304.gif) 得,
得, 数学文科.files/image306.gif) ,
,数学文科.files/image308.gif) ,???10分
,???10分
故数学文科.files/image310.gif) ,???11分
,???11分
二面角数学文科.files/image157.gif) 的大小为
的大小为数学文科.files/image312.gif) 。???12分
。???12分
(其他解法酌情给分)
19(13分). 解:(Ⅰ)数学文科.files/image314.gif) ,
,
∴当数学文科.files/image316.gif) 时,
时,数学文科.files/image318.gif) 。???2分
。???2分
当数学文科.files/image320.gif) 时,
时,数学文科.files/image322.gif) ,???4分
,???4分
当数学文科.files/image316.gif) 时也满足上式,故
时也满足上式,故
数列数学文科.files/image096.gif) 的通项公式是
的通项公式是数学文科.files/image324.gif) 。???6分(未验算减1分)
。???6分(未验算减1分)
(Ⅱ)数学文科.files/image326.gif) ,???7分
,???7分
数学文科.files/image328.gif) ①
①
数学文科.files/image330.gif) ②
②
①
-②得数学文科.files/image332.gif)
数学文科.files/image334.gif) ,
,
数学文科.files/image336.gif) 。???9分(有错位相减思想,计算错误得1分,后继过程不计分)
。???9分(有错位相减思想,计算错误得1分,后继过程不计分)
数学文科.files/image338.gif) ,
,
数学文科.files/image340.gif) 数列
数列数学文科.files/image342.gif) 单调递增,
单调递增,数学文科.files/image344.gif) 最小,最小值为:
最小,最小值为:数学文科.files/image346.gif) ???11分
???11分
数学文科.files/image348.gif) ???12分
???12分
故正整数数学文科.files/image178.gif) 的最大值为2。???13分
的最大值为2。???13分
20.解:(Ⅰ)∵数学文科.files/image190.gif) ,
,
∴数学文科.files/image351.gif) ,即
,即数学文科.files/image353.gif) ,
,
∴数学文科.files/image355.gif) 。----3分
。----3分
设数学文科.files/image357.gif) ,则
,则数学文科.files/image359.gif) ,
,数学文科.files/image361.gif) ,
,
平方整理得曲线C的方程:数学文科.files/image363.gif) 。-----6分
。-----6分
(Ⅱ)由曲线C的对称性知,以N为中点的弦的斜率存在,设弦的端点为数学文科.files/image365.gif) ,则
,则数学文科.files/image367.gif) 。-----8分
。-----8分
∵点A、B都在曲线C上,
数学文科.files/image369.gif) ,
,
两式相减得:数学文科.files/image371.gif) ,----10分
,----10分
数学文科.files/image373.gif) ,
,
∴弦AB的斜率数学文科.files/image375.gif) ,12分
,12分
∴弦AB的直线方程为数学文科.files/image377.gif) ,即
,即数学文科.files/image379.gif) 。???13分
。???13分
21(13分). 解:(Ⅰ)数学文科.files/image381.gif) ,???1分
,???1分
数学文科.files/image383.gif) ,???2分
,???2分
故函数数学文科.files/image094.gif) 在区间
在区间数学文科.files/image386.gif) 、
、数学文科.files/image388.gif) 上单调递增,
上单调递增,
在数学文科.files/image390.gif) 上单调递减。???4分
上单调递减。???4分
(Ⅱ)∵二次函数数学文科.files/image201.gif) 有最大值,
有最大值,数学文科.files/image392.gif) 。???5分
。???5分
由数学文科.files/image394.gif) 得
得数学文科.files/image396.gif) ,???6分
,???6分
∵函数数学文科.files/image206.gif) 与
与数学文科.files/image208.gif) 的图象只有一个公共点,
的图象只有一个公共点,
数学文科.files/image398.gif) 。
。
又数学文科.files/image203.gif) ,
,数学文科.files/image401.gif) 。???7分
。???7分
又数学文科.files/image403.gif) ,
,数学文科.files/image405.gif)
数学文科.files/image407.gif) 。???8分
。???8分
(Ⅲ)当数学文科.files/image203.gif) 时,函数
时,函数数学文科.files/image094.gif) 在区间
在区间数学文科.files/image386.gif) 、
、数学文科.files/image388.gif) 上单调递增,
上单调递增,
函数数学文科.files/image210.gif) 在区间
在区间数学文科.files/image410.gif) 上单调递增。
上单调递增。
数学文科.files/image412.gif) ,解得
,解得数学文科.files/image414.gif) 。???10分
。???10分
当数学文科.files/image416.gif) 时,函数
时,函数数学文科.files/image094.gif) 在区间
在区间数学文科.files/image418.gif) 、
、数学文科.files/image420.gif) 上单调递增,
上单调递增,
函数数学文科.files/image210.gif) 在区间
在区间数学文科.files/image422.gif) 上单调递增。
上单调递增。
数学文科.files/image424.gif) ,解得
,解得数学文科.files/image426.gif) 。???12分
。???12分
综上所述,实数数学文科.files/image072.gif) 的取值范围是
的取值范围是数学文科.files/image428.gif) 。???13分
。???13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com