
题目列表(包括答案和解析)
 的图象上各点的横坐标伸长到原来的2倍,再向左平移
的图象上各点的横坐标伸长到原来的2倍,再向左平移 个单位,得到的函数图象的一条对称轴方程是( )
个单位,得到的函数图象的一条对称轴方程是( )



将函数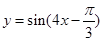 的图像上各点的横坐标伸长到原来的2倍,再向左平移
的图像上各点的横坐标伸长到原来的2倍,再向左平移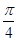 个单位,得到的函数的一条对称轴是
个单位,得到的函数的一条对称轴是
A.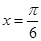 B.
B.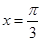 C.
C.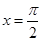 D.
D.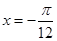
将函数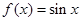 图象上所有点的横坐标伸长到原来的2倍,再向右平移
图象上所有点的横坐标伸长到原来的2倍,再向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,则
的图象,则 图象的解析式是( )
图象的解析式是( )
A. | B. |
C. | D. |
将函数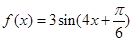 图象上所有点的横坐标伸长到原来的2倍,再向右平移
图象上所有点的横坐标伸长到原来的2倍,再向右平移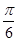 个单位长度,得到函数
个单位长度,得到函数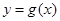 的图象,则
的图象,则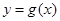 图象的一条对称轴是( )
图象的一条对称轴是( )
A.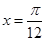 | B.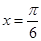 | C.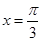 | D.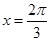 |
 图象上所有点的横坐标伸长到原来的2倍,再向右平移
图象上所有点的横坐标伸长到原来的2倍,再向右平移 个单位长度,得到函数
个单位长度,得到函数 的图象,则
的图象,则 图象的解析式是( )
图象的解析式是( )A. | B. |
C. | D. |
一、选择题:本大题共12小题,每小题5分,共60分。
1―6ACAABB 7―12DCDACD
二、填空题:本大题共4小题,每小题5分,共20分。
13.60° 14.40 15. 16.6
16.6
|