一、选择题:本大题共12小题,每小题5分,共60分。
1―6ACAABB 7―12DCDACD
二、填空题:本大题共4小题,每小题5分,共20分。
13.60° 14.40 15. 16.6
16.6
20090411 17.(本小题满分10分)
(I)解:因为 由正弦定理得 所以 又 故 5分 5分
(II)由 故  10分 10分 18.(本小题满分12分)
(I)解:设等差数列 由 成等比数列, 成等比数列, 得 即 得 (舍去)。 (舍去)。 故 所以 6分 6分
(II)又 则 又 故 的等差数列。 的等差数列。 所以 12分 12分 19.(本小题满分12分) 解:设事件 则
(I)设“赛完两局比赛结束”为事件C,则 则 即  因为 所以 因为 6分 6分
(II)设“赛完四局比赛结束且乙比甲多2分”为事件D, 则 即   = 12分
12分 20.(本小题满分12分)
(I)证明:  2分 2分 又

(II)方法一 解:过O作  则O1是ABC截面圆的圆心,且BC是直径, 过O作 于M,则M为PA的中点, 于M,则M为PA的中点, 连结O1A,则四边形MAO1O为矩形,  8分 8分 过O作 于E,连EO1, 于E,连EO1, 则 为二面角O―AC―B的平面角 10分 为二面角O―AC―B的平面角 10分 在  在 所以二面角O―AC―B的大小为 12分 12分 方法二

同上, 8分 8分    设面OAC的法向量为  得 故 所以二面角O―AC―B的大小为 12分 12分 21.(本小题满分12分)
(I)解:当 故 1分 1分 因为 当 当 故 上单调递减。
5分 上单调递减。
5分
(II)解:由题意知 上恒成立, 上恒成立, 即 上恒成立。
7分 上恒成立。
7分 令 因为 9分 9分 故 上恒成立等价于 上恒成立等价于  11分 11分 解得 12分 12分 22.(本小题满分12分) 解:依题意设抛物线方程为 , , 直线 则 的方程为 的方程为  因为 即 故
(I)若 得 得  故点B的坐标为 所以直线 5分 5分
(II)联立 得 得  则 又 7分 7分 故 9分 9分 因为 成等差数列, 成等差数列, 所以 故 即 即 将 代入上式得 代入上式得  由 由 。 12分 。 12分
| | | | | |



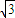 -1
-1


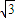 -1
-1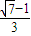


 -1
-1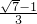

 16.6
16.6