
题目列表(包括答案和解析)
 已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,
已知抛物线的顶点在坐标原点O,焦点F在x轴正半轴上,倾斜角为锐角的直线l过F点,设直线l与抛物线交于A、B两点,与抛物线的准线交于M点,| MF |
| FB |
| B1F |
| OF |
| A1F |
已知抛物线的顶点在坐标原点O,焦点F在x正半轴上,倾斜角为锐角的直线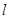 过F点。设直线
过F点。设直线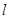 与抛物线交于A、B两点,与抛物线的准线交于M点,
与抛物线交于A、B两点,与抛物线的准线交于M点,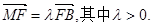
(I)若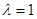 ,求直线
,求直线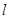 的斜率;
的斜率;
(II)若点A、B在x轴上的射影分别为A1、B1,且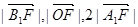 成等差数列,求
成等差数列,求 的值。
的值。
| MF |
| FB |
| B1F |
| OF |
| A1F |
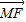 =λ
=λ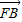 (λ>0)
(λ>0)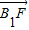 |,|
|,|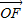 |,2|
|,2|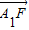 |成等差数列求λ的值
|成等差数列求λ的值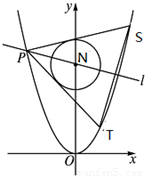
| MF |
| FB |
| B1F |
| OF |
| A1F |
一、选择题:本大题共12小题,每小题5分,共60分。
1―6ACAABB 7―12DCDACD
二、填空题:本大题共4小题,每小题5分,共20分。
13.60° 14.40 15. 16.6
16.6
|