
题目列表(包括答案和解析)
设![]()
(I)求![]() 在
在![]() 上的最小值;
上的最小值;
(II)设曲线![]() 在点
在点![]() 的切线方程为
的切线方程为![]() ;求
;求![]() 的值。
的值。
设![]()
(I)求![]() 在
在![]() 上的最小值;
上的最小值;
(II)设曲线![]() 在点
在点![]() 的切线方程为
的切线方程为![]() ;求
;求![]() 的值。
的值。
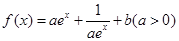
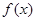 在
在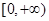 上的最小值;
上的最小值;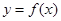 在点
在点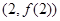 的切线方程为
的切线方程为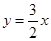 ;求
;求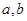 的值。
的值。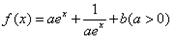 ;
;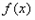 在
在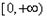 上的最小值;
上的最小值; 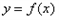 在点
在点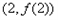 的切线方程为
的切线方程为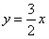 ;求
;求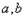 的值。
的值。已知函数 .
.
(I)判断 的奇偶性;
的奇偶性;
(Ⅱ)设函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的表达式;
的表达式;
(Ⅲ)若 ,证明:方程
,证明:方程 有两个不同的正数解.
有两个不同的正数解.
一、选择题:本大题共12小题,每小题5分,共60分。
1―6AABCBD 7―12ACDCBD
二、填空题:本大题共4小题,每小题5分,共20分。
13.60° 14.-8 15. 16.6
16.6
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)
(I)解:因为
由正弦定理得
所以
又
故 5分
5分
(II)由
故
 10分
10分
18.(本小题满分12分)
(I)解:当
故 1分
1分
因为 当
当
故 上单调递减。
5分
上单调递减。
5分
(II)解:由题意知 上恒成立,
上恒成立,
即 上恒成立。
7分
上恒成立。
7分
令
因为 9分
9分
故 上恒成立等价于
上恒成立等价于
 11分
11分
解得 12分
12分
19.(本小题满分12分)
(I)证明:
 2分
2分
又
|