
题目列表(包括答案和解析)
(本小题满分12分)
某次国际象棋友谊赛在中国队和乌克兰队之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,根据以往战况,每局中国![]() 队赢的概率为
队赢的概率为![]() ,乌克兰队赢的概率为
,乌克兰队赢的概率为![]() ,且每局比赛输赢互不影响.若中国队第n局的得分记为
,且每局比赛输赢互不影响.若中国队第n局的得分记为![]() ,令
,令![]() .
.
(1)求![]() 的概率;
的概率;
(2)若规定:当其中一方的积分达到或超过4分时,比赛不再继续,否则,继续进行.设随机变量![]() 表示此次比赛共进行的局数,求
表示此次比赛共进行的局数,求![]() 的分布列及数学期望.
的分布列及数学期望.
(本小题满分12分)
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
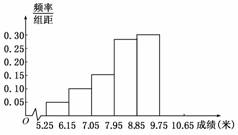 (1) 求这次铅球测试成绩合格的人数;
(1) 求这次铅球测试成绩合格的人数;
(2) 用此次测试结果估计全市毕业生的情况.若从今年的高中毕业生中随机抽取两名,记![]() 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3) 经过多次测试后,甲成绩在8~10米之间,乙成绩在9.5~10.5米之间,现甲、乙各投掷一次,求甲比乙投掷远的概率.
(本小题满分12分)从甲、乙两名运动员的若干次训练成绩中随机抽取6次,分别为甲:7.7,7.8,8.1,8.6,9.3,9.5.乙:7.6,8.0,8.2,8.5,9.2,9.5

(1)根据以上的茎叶图,对甲、乙运动员的成绩作比较,写出两个统计结论;
(2)从甲、乙运动员六次成绩中各随机抽取1次成绩,求甲、乙运动员的成绩至少有一个高于8.5分的概率。
(3)经过对甲、乙运动员若干次成绩进行统计,发现甲运动员成绩均匀分布在[7.5,9.5]之间,乙运动员成绩均匀分布在[7.0,10]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.5分的概率。
(本小题满分12分)函数f(x)=ax2-2(a-1)x-2lnx ,a>0
(1)求函数f(x)的单调区间;
(2)对于函数图像上的不同两点A(x1,y1),B(x2,y2),如果在函数图像上存在点P(x0,y0)(其中x0在x1与x2之间),使得点P处的切线l平行于直线AB,则称AB存在“伴随切线”,当x0= 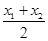 时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
时,又称AB存在“中值伴随切线”.试问:在函数f(x)的图像上是否存在不同两点A,B,使得AB存在“中值伴随切线”?若存在,求出A,B的坐标;若不存在,说明理由
(本小题满分12分)
如图,面积为 的正方形
的正方形 中有一个不规则的图形M,可按下面方法估计M的面积:在正方形
中有一个不规则的图形M,可按下面方法估计M的面积:在正方形 中随机投掷
中随机投掷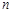 个点,若
个点,若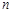 个点中有
个点中有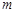 个点落入M中,则M的面积的估计值为
个点落入M中,则M的面积的估计值为 . 假设正方形
. 假设正方形 的边长为2,M的面积为1,并向正方形
的边长为2,M的面积为1,并向正方形 中随机投掷10 000个点,以
中随机投掷10 000个点,以 表示落入M中的点的数目.
表示落入M中的点的数目.
(Ⅰ)求 的均值
的均值 ;
;
 (Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间
(Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间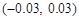 内的概率.
内的概率.
附表: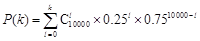
|
|
2424 |
2425 |
2574 |
2575 |
|
|
0.0403 |
0.0423 |
0.9570 |
0.9590 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com