
题目列表(包括答案和解析)
设函数
(1)当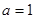 时,求曲线
时,求曲线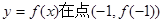 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数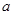 的取值范围.
的取值范围.
【解析】(1)中,先利用 ,表示出点
,表示出点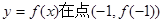 的斜率值
的斜率值 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当 ,再令
,再令 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当 ……2分
……2分
 ∴
∴
即 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令 ………………6分
………………6分
∴ 递减,在(3,+
递减,在(3,+ )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)
①若 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数 的取值范围是
的取值范围是
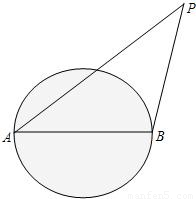
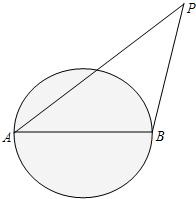 外轮除特许外,不得进入离我国海岸线12海里以内的区域,如图:我国某海岛海岸线是半径为6海里的圆形区域,在直径的两个端点A、B设立两个观察点,已知一外轮在点P处,测得∠BAP=α,∠ABP=β.
外轮除特许外,不得进入离我国海岸线12海里以内的区域,如图:我国某海岛海岸线是半径为6海里的圆形区域,在直径的两个端点A、B设立两个观察点,已知一外轮在点P处,测得∠BAP=α,∠ABP=β.2009年5月11日,中国内地出现首例输入性甲型H1N1流感疑似病例。中国进入防控甲型H1N1流感的关键时期,到目前为止,中国在防控方面取得了令人满意的成绩。据统计:公众对我国防控甲型H1N1流感的满意率![]() ,(不满意率为
,(不满意率为![]() ,
,![]() ),现随机从人群中抽出
),现随机从人群中抽出![]() 个人调查对我国防控甲型H1N1流感的满意度,用随机变量
个人调查对我国防控甲型H1N1流感的满意度,用随机变量![]() 表示调查的这些人中的不满意的人数.
表示调查的这些人中的不满意的人数.
(1)当![]() ,
,![]() ,列出随机变量
,列出随机变量![]() 的分布列,并求出随机变量
的分布列,并求出随机变量![]() 的数学期望
的数学期望![]() ;
;
(2)试证明:![]() =
=![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com