
题目列表(包括答案和解析)
用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃(不一定用完每一种颜色的鲜花),要求同一区域上用同一种颜色的鲜花,相邻区域用不同颜色的鲜花.

①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为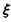 求
求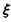 的分布列和数学期望E
的分布列和数学期望E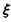
用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃(不一定用完每一种颜色的鲜花),要求同一区域上用同一种颜色的鲜花,相邻区域用不同颜色的鲜花.
①求恰有两个区域用红色鲜花的概率;
 ②记花圃中红色鲜花区域的块数为
②记花圃中红色鲜花区域的块数为![]() 求
求![]() 的分布列和数学期望E
的分布列和数学期望E![]()

 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率;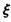 求
求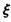 的分布列和数
的分布列和数 学期望E
学期望E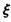
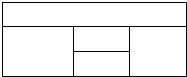 [理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
[理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花. [理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
[理]用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
B
C
B
C
A
C
A
B
C
D
二、填空题
13. 192 14. 15 15.  16. ②③⑤
16. ②③⑤
三、解答题
17. 解:(Ⅰ)设三角形三内角A、B、C对应的三边分别为a, b, c,
∵ ,∴
,∴ ,由正弦定理有
,由正弦定理有 ,………………3分
,………………3分
又由余弦定理有 ,∴
,∴ ,即
,即 ,
,
所以 为Rt
为Rt ,且
,且 . ………………6分
. ………………6分
(Ⅱ)又 , 令a=4k, b=3k
(k>0). ………………8分
, 令a=4k, b=3k
(k>0). ………………8分
 则
则 ,∴三边长分别为a=4,b=3,c=5. ………………10分
,∴三边长分别为a=4,b=3,c=5. ………………10分
 18. (Ⅰ)如图,首先从五种不同颜色的鲜花中任选四种共
18. (Ⅰ)如图,首先从五种不同颜色的鲜花中任选四种共 种,
种,
用四种颜色鲜花布置可分两种情况:区域A、D同色和区域B、E同色,
 皆有
皆有 种,………………3分
种,………………3分
故恰用四种不同颜色的鲜花布置的不同摆放方案共有 种. ………………6分
种. ………………6分
(Ⅱ)设M表示事件“恰有两个区域用红色鲜花”,
如图,当区域A、D同色时,共有 种;
种;
当区域A、D不同色时,共有 种;
种;
因此,所有基本事件总数为:180+240=420种. ………………8分
它们是等可能的.又因为A、D为红色时,共有 种;
种;
B、E为红色时,共有 种;
种;
因此,事件M包含的基本事件有:36+36=72种.………………10分
所以,恰有两个区域用红色鲜花的概率 =
= .………………12分
.………………12分
19. (Ⅰ)延长 至M,使
至M,使 ,连
,连 ,则
,则 ,连
,连 ,则
,则 或其补角就是异面直线
或其补角就是异面直线 与
与 所成角(设为
所成角(设为 ),………………2分
),………………2分
 不妨设AA1=AB=1,则在
不妨设AA1=AB=1,则在 中,
中, ,
,
所以
故异面直线 与
与 所成角的余弦值为
所成角的余弦值为 .………………6分
.………………6分
(Ⅱ)
 是正三棱柱,
是正三棱柱,
 平面
平面 ,
,

 平面
平面 ,
, 平面
平面
 平面
平面 ,
,
过点 作
作
 于点
于点 ,则
,则
 平面
平面 ,
,
过 作
作 于
于 ,由三垂线定理得
,由三垂线定理得 ,
,
故∠ 为二面角
为二面角 的平面角. ………………9分
的平面角. ………………9分
 不妨设AA1=AB=2,
不妨设AA1=AB=2,
 则
则 ,在
,在 △
△ 中,
中, .
.
 二面角
二面角 的正弦值为
的正弦值为 .………………12分
.………………12分
20. 解:(Ⅰ)由已知,当 时,
时, ……………… 2分
……………… 2分
 . 经检验
. 经检验 时也成立. ………………4分
时也成立. ………………4分
由 ,得
,得 ,∴p=
,∴p= .
.
∴  .……………… 6分
.……………… 6分
(Ⅱ)由(1)得, . ……………… 7分
. ……………… 7分
 2 ; ①
2 ; ①
 . ② ………………9分
. ② ………………9分
②-①得,
= =
= . ………………12分
. ………………12分
21. 解:(Ⅰ)f′(x)=3ax2+2bx-3,依题意,f′(1)=f′(-1)=0,………………2分
即 解得a=1,b=0.∴f(x)=x3-3x. ………………4分
解得a=1,b=0.∴f(x)=x3-3x. ………………4分
(Ⅱ)f′(x)=3x2-3=3(x+1)(x-1),
∵曲线方程为y=x3-3x,∴点A(1,m)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足
因 ,故切线的斜率为
,故切线的斜率为 ,
,
整理得 .………………7分
.………………7分
∵过点A(1,m)可作曲线的三条切线,
∴关于x0的方程 =0有三个实根.
=0有三个实根.
 设g(x0)=
设g(x0)=  ,则g′(x0)=6
,则g′(x0)=6 ,
,
由g′(x0)=0,得x0=0或x0=1. ………………9分
∴g(x0)在(-∞,0),(1,+∞)上单调递增,在(0,1)上单调递减.
 ∴函数g(x0)=
∴函数g(x0)=  的极值点为x0=0,x0=1.
的极值点为x0=0,x0=1.
∴关于x0方程 =0有三个实根的充要条件是
=0有三个实根的充要条件是
解得-3<m<-2.
故所求的实数a的取值范围是-3<m<-2. ………………12分
22. 解:(Ⅰ)∵ ,
,
设O关于直线  的对称点为
的对称点为 的横坐标为
的横坐标为  ,………………2分
,………………2分
又直线 得线段
得线段 的中点坐标(1,-3).
的中点坐标(1,-3).
∴ ,
,
∴椭圆方程为 .………………5分
.………………5分
(Ⅱ)设点 ,当直线l的斜率存在时,
,当直线l的斜率存在时,
则直线l的方程为 ,………6分
,………6分
代入 得:
得:
 , ……①
, ……①
又  ,①可化为:
,①可化为:
 ,………………8分
,………………8分
由已知,有 
 ,
,
∵ ………………10分
………………10分

 同理
同理
解得  ,
,
∴ ……………………11分
……………………11分
故直线ME垂直于x轴,由椭圆的对称性知点M、E关于x轴对称,而点B在x轴上,
∴|BM|=|BE|,即△BME为等腰三角形.
当直线l的斜率不存在时,结论显然成立.……………………12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com