
题目列表(包括答案和解析)
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由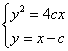 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由条件
,由条件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .从而,
.从而,![]() :
:![]() ,即
,即![]() .
.
由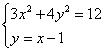 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
解关于 的不等式
的不等式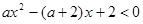
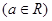
【解析】本试题主要考查了含有参数的二次不等式的求解,
首先对于二次项系数a的情况分为三种情况来讨论,
A=0,a>0,a<0,然后结合二次函数的根的情况和图像与x轴的位置关系,得到不等式的解集。
解:①若a=0,则原不等式变为-2x+2<0即x>1
此时原不等式解集为 ;
; 
②若a>0,则ⅰ)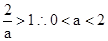 时,原不等式的解集为
时,原不等式的解集为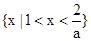 ;
;
ⅱ) 时,原不等式的解集为
时,原不等式的解集为 ;
;
ⅲ)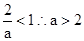 时,原不等式的解集为
时,原不等式的解集为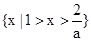 。
。 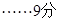
③若a<0,则原不等式变为
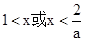 原不等式的解集为
原不等式的解集为 。
。
解析:依题意得f(x)的图象关于直线x=1对称,f(x+1)=-f(x-1),f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),即函数f(x)是以4为周期的函数.由f(x)在[3,5]上是增函数与f(x)的图象关于直线x=1对称得,f(x)在[-3,-1]上是减函数.又函数f(x)是以4为周期的函数,因此f(x)在[1,3]上是减函数,f(x)在[1,3]上的最大值是f(1),最小值是f(3).
答案:A
解析 第二列等式的右端分别是1×1,3×3,6×6,10×10,15×15,∵1,3,6,10,15,…第n项an与第n-1项an-1(n≥2)的差为:an-an-1=n,∴a2-a1=2,a3-a2=3,a4-a3=4,…,an-an-1=n,各式相加得,
an=a1+2+3+…+n,其中a1=1,∴an=1+2+3+…+n,即an=![]() ,∴a
,∴a![]() =
=![]() n2(n+1)2.
n2(n+1)2.
答案 ![]() n2(n+1)2
n2(n+1)2
解答题:解答应写出文字说明、证明过程或演算步骤.
美国蓝球职业联赛(NBA)某赛季的总决赛在湖人队与活塞队之间进行,比赛采取七局四胜制,即若有一队胜四场,则此队获胜且比赛结束.因两队实力非常接近,在每场比赛中每队获胜是等可能的.据资料统计,每场比赛组织者可获门票收入100万美元.求在这次总决赛过程中,比赛组织者获得门票收入![]() (万美元)的概率分布及数学期望
(万美元)的概率分布及数学期望![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com