题目列表(包括答案和解析)
(本小题满分12分)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行
测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.
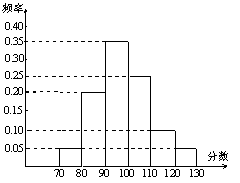
抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120～130
(包括120分但不包括130分)的频率为0.05, 此分数段的人数为5人.
（1）问各班被抽取的学生人数各为多少人?
（2）在抽取的所有学生中,
任取一名学生, 求分数
不小于90分的概率.
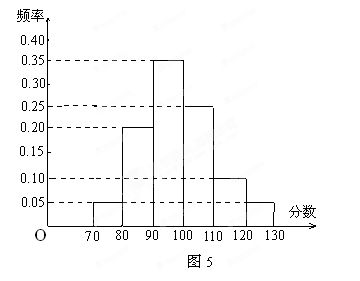
(本小题满分12分) 某校高三文科分为五个班.高三数学测试后, 随机地在各班抽取部分学生进行成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了18人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中120～130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.
(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.
 |
(本小题满分12分)
为适应新课改，切实减轻学生负担，提高学生综合素质，怀化市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革，由学生自由选择2门（不可多选或少选），选课情况如下表：
| 4-4 | 4-5 | 4-7 | |
| 男生 | 130 |
| 80 |
| 女生 |
| 100 | 60 |
（1）为了解学生情况，现采用分层抽样方法抽取了三科作业共50本，统计发现4-5有18本，
试根据这一数据求出
，
的值。
（2）为方便开课，学校要求
，
，计算
的概率。
（本小题满分12分）
某中学研究性学习小组，为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了 50名学生.调査结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般.
（Ⅰ）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？
高中学生的作文水平与爱看课外书的2×2列联表
|
|
爱看课外书 |
不爱看课外书 |
总计 |
|
作文水平好 |
|
|
|
|
作文水平一般 |
[来源:学。科。网Z。X。X。K] |
|
|
|
总计 |
|
|
|
（Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5，某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
参考公式：
，其中
.
参考数据：
|
|
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
一、选择题：本大题主要考查基本知识和基本运算．共10小题，每小题5分，满分50分．
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
A
B
C
D
C
B
D
二、填空题：本大题主要考查基本知识和基本运算．本大题共5小题，考生作答4小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题．
11．
12．
13．
14．
15．2
说明：第14题答案可以有多种形式，如可答
或
Z）等, 均给满分.
三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.
16．(本小题满分12分)
解：（1）∵
.
6分
∴
.
8分
(2) 当
时, 
取得最大值, 其值为2 . ……………………10分
此时
，即
Z
. ……………………12分
17. (本小题满分12分)
解:(1) 由频率分布条形图知,抽取的学生总数为
人. ………… 3分
∵各班被抽取的学生人数成等差数列,设其公差为
,
由
=100,解得
. …………………………………… 6分
∴各班被抽取的学生人数分别是22人，24人，26人，28人. …… 8分
(2) 在抽取的学生中,任取一名学生, 则分数不小于90分的概率为0.35+0.25+0.1+0.05=0.75. ………………………………12分
18．(本小题满分14分)
解：（1）∵ 
⊥平面
，
平面，
∴
⊥.
………………………………………………2分
∵
⊥
，
，
∴
⊥平面
， ……………………………………………………4分
∵
平面，
∴
⊥. …………………………………………………………6分
（2）法1: 取线段
的中点
，
的中点
，连结
,
则
是△
中位线.
∴∥
，
， …………………………8分
∵
，
，
∴
.
∴
四边形
是平行四边形， …………………………10分
∴ 
.
∵ 
平面
，
平面，
∴ ∥平面. …………………………………… 13分
∴
线段的中点是符合题意要求的点． ……………………………………14分
法2: 取线段的中点，的中点，连结
,
则是△的中位线.
∴∥，
， …………………………8分
∵
平面, 
平面,
∴
平面.
∵
，，
∴
.
∴
四边形
是平行四边形， ……………………………………10分
∴ 
.
∵ 
平面，
平面，
∴ ∥平面
.
∵
,
∴平面
平面.……………………………………………………12分
∵
平面
,
∴∥平面.
∴
线段的中点是符合题意要求的点．……………………………… 14分
19. (本小题满分14分)
解:(1)依题意知,
…………………………………………2分
∵
,
∴
. ………………………………………… 5分
∴所求椭圆
的方程为
. …………………………………………6分
（2）∵ 点
关于直线
的对称点为
，
∴ 
解得：
，
.
…………………………8分
∴
.
……………………………10分
∵
点在椭圆:上,
∴
, 则
.………………………………………………12分
∴
的取值范围为
. …………………………………………14分
20. (本小题满分14分)
(1) 解：当
时，
.
……………………………………1分
当
时，
.
…………………………………………4分
∵
不适合上式,
∴
………………………………………………………5分
（2）证明: ∵
.
当
时，
………………………………………………6分
当时，
,
①
. ②
①－②得:
得
， …………………………………………10分
此式当时也适合.
∴
N
.
∵
，
∴
.
…………………………………………………11分
当时，
，
∴
.
∵
，
∴
.
故
，即
. ……………………………………………13分
综上，
．
………………………………14分
21. (本小题满分14分)
解：（1）当
时，
，
∴
.
令=0, 得 
.
………………………………………………2分
当
时,
, 则
在
上单调递增;
当
时,
, 则在
上单调递减;
当
时,, 在
上单调递增.
…………………………2分
∴ 当
时, 取得极大值为
;…………………………4分
当
时, 取得极小值为
. ………………………6分
（2） ∵ = 
，
∴△= 
= 
.
① 若a≥1，则△≤0，
∴≥0在R上恒成立，
∴ f（x）在R上单调递增 .
∵f（0）
，
,
∴当a≥1时，函数f（x）的图象与x轴有且只有一个交点． ……………………9分
② 若a＜1，则△＞0，
∴= 0有两个不相等的实数根，不妨设为x1，x2，（x1<x2）．
∴x1+x2 = 2，x1x2 = a．
当
变化时，
的取值情况如下表：
x
x1
（x1，x2）
x2
+
0
－
0
+
f（x）
ㄊ
极大值
ㄋ
极小值
ㄊ
∵
,
∴
.
∴
.
同理
.
∴
.
令f（x1）?f（x2）＞0, 解得a＞
．
而当
时,
,
故当时, 函数f（x）的图象与x轴有且只有一个交点.
综上所述，a的取值范围是
．
……………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
[来源:学*科*网]