查看答案和解析>>

查看答案和解析>>

已知数列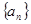中，，且满足，．
（I）求数列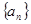的通项公式；
（II）设为非零整数，），试确定的值，使得对任意，都有成立．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

1. －               2.             3.             4.

5.                6. 或    7. ④             8.

9.    10. （２，４］       11. （28，44）      12.

13. 5                14. m>

15.（1）【证明】∵△PAB中， D为AB中点，M为PB中点，∴

∵DM平面，PA平面，∴平面            ……3分

（2）【证明】∵D是AB的中点，△PDB是正三角形，AB=20，

∴                ……4分

∴△PAB是直角三角形，且AP⊥PB，……5分

又∵AP⊥PC，……6分

∴AP⊥平面PBC．∴AP⊥BC．……8分

又∵AC⊥BC， AP∩AC=A，∴BC⊥平面PAC．……9分

∵ ∴平面PAC⊥平面ABC．……10分

（3）【解】由（1）知，由（2）知PA⊥平面PBC， 

∴DM⊥平面PBC．……11分

∵正三角形PDB中易求得，

 ……13分

∴……14分

16．解：（Ⅰ）∵

   ………………………………………………………………4分

又∵   ……………………………………6分

即 

∴y_max=5，  y_min=3   …………………………………………………………………8分

（Ⅱ）∵  ……………………………10分

又∵P为q的充分条件 ∴   ………………………………………13分 

解得  3<m<5    ……………………………………………………………………14分

17. 解：（1）由题意知，需加工G型装置4000个，加工H型装置3000个，所用工人分别为x人，（216－x）人.

∴g（x）=，h（x）=，

即g（x）=，h（x）=（0＜x＜216，x∈N^*）. ……………………4分

（2）g（x）－h（x）=－=.

∵0＜x＜216，

∴216－x＞0.

当0＜x≤86时，432－5x＞0，g（x）－h（x）＞0，g（x）＞h（x）；

当87≤x＜216时，432－5x＜0，g（x）－h（x）＜0，g（x）＜h（x）.

∴f（x）= ……………………8分

（3）完成总任务所用时间最少即求f（x）的最小值.

当0＜x≤86时，f（x）递减，

∴f（x）≥f（86）==.

∴f（x）_min=f（86），此时216－x=130.

当87≤x＜216时，f（x）递增，

∴f（x）≥f（87）==.

∴f（x）_min=f（87），此时216－x=129.

∴f（x）_min=f（86）=f（87）=.

∴加工G型装置，H型装置的人数分别为86、130或87、129……………………14分

18. （Ⅰ）由题设知

由于，则有，所以点的坐标为……..2分

故所在直线方程为…………3分

所以坐标原点到直线的距离为

又，所以  解得： …………5分

所求椭圆的方程为…………6分

（Ⅱ）由题意可知直线的斜率存在，设直线斜率为

直线的方程为，则有…………8分

设，由于、、三点共线，且

根据题意得,解得或…………14分

又在椭圆上，故或

解得,综上，直线的斜率为或     …………16分

19. 解：（1）由已知，（，），

即（，），且．

∴数列是以为首项，公差为1的等差数列．

∴．

（2）∵，∴，要使恒成立，

∴恒成立，

∴恒成立，

∴恒成立．

（?）当为奇数时，即恒成立，

当且仅当时，有最小值为1，

∴．

（?）当为偶数时，即恒成立，

当且仅当时，有最大值，

∴．

即，又为非零整数，则．

综上所述，存在，使得对任意，都有．

20.解：（I）                            2分

由得，或

而，列出下表

0

―

0

+

0

―

递减

极小值

递增

极大值

递减

所以，当时，取得极小值，极小值等于；

当时，取得极大值，极大值等于；                 6分

（II）设函数、，    不妨设

      （注：若直接用来证明至少扣1分）                           10分

（III）时，

                                                                16分