
题目列表(包括答案和解析)
![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
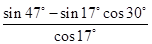
(A)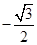 (B)
(B)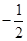 (C)
(C)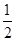 (D)
(D)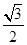
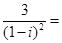
(A)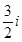 (B)
(B)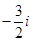 (C)
(C)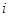 (D)
(D)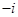
1、B
2、D
3、A
4、[解法一]设
而
又∵ 在复平面上对应的点在第二、四象限的角平分线上,
在复平面上对应的点在第二、四象限的角平分线上,
∴ ,得
,得 .
.
∴ . 即
. 即 ;
; ,
,
当 时,有
时,有 ,即
,即 ,得
,得 .
.
当 时,同理可得
时,同理可得 .
.
[解法二] ,∴
,∴ ,
,
得
或
 得
得 .
.
当 时,有
时,有 ,即
,即 ,得
,得 .
.
当 时,同理可得
时,同理可得 .
.
5、解:由
由 得
得
故

当且仅当 时,即
时,即 时,上式取等号.
时,上式取等号.
所以当 时,函数
时,函数 取最大值
取最大值
6、D
7、解:因为
因为
于是
由此得OP⊥OQ,|OP|=|OQ| .
由此知△OPQ有两边相等且其夹角为直角,故△OPQ为等腰直角三角形。
8、B
9、解:设Z1,Z3对应的复数分别为
依题设得


10、A
11、(1)
(2)
12、 ,
, 或
或
13、解:(Ⅰ)由 

 ,
,
得 . ……4分
. ……4分
因为  ,
, ,
,
所以  . ……6分
. ……6分
(Ⅱ)因为 ,
,
所以  ,而
,而 ,所以
,所以 ,
,
 ,同理
,同理 ,
, .
.
由(Ⅰ)知  ,
,
即  ,
,
所以  的实部为
的实部为 , ……8分
, ……8分
而 的辐角为
的辐角为 时,复数
时,复数 的实部为
的实部为
 ,
,
所以  ……12分
……12分
14、C
15、[解](1)由题设, ,
,
于是由 ,
…(3分)
,
…(3分)
因此由 ,
,
得关系式 …(5分)
…(5分)
[解](2)设点 在直线
在直线 上,则其经变换后的点
上,则其经变换后的点 满足
满足
 ,
…(7分)
,
…(7分)
消去 ,得
,得 ,
,
故点 的轨迹方程为
的轨迹方程为 …(10分)
…(10分)
[解](3)假设存在这样的直线,∵平行坐标轴的直线显然不满足条件,
∴所求直线可设为 ,
…(12分)
,
…(12分)
[解法一]∵该直线上的任一点 ,其经变换后得到的点
,其经变换后得到的点
 仍在该直线上,
仍在该直线上,
∴ ,
,
即 ,
,
当 时,方程组
时,方程组 无解,
无解,
故这样的直线不存在。 …(16分)
当 时,由
时,由
得 ,
,
解得 或
或 ,
,
故这样的直线存在,其方程为 或
或 ,
…(18分)
,
…(18分)
[解法二]取直线上一点 ,其经变换后的点
,其经变换后的点 仍在该直线上,
仍在该直线上,
∴ ,
,
得 ,
…(14分)
,
…(14分)
故所求直线为 ,取直线上一点
,取直线上一点 ,其经变换后得到的点
,其经变换后得到的点 仍在该直线上。
仍在该直线上。
∴ ,
…(16分)
,
…(16分)
即 ,得
,得 或
或 ,
,
故这样的直线存在,其方程为 或
或 ,
…(18分)
,
…(18分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com