
题目列表(包括答案和解析)
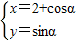 (α为参数)上任意一点,则(x-5)2+(y+4)2的最大值为 .
(α为参数)上任意一点,则(x-5)2+(y+4)2的最大值为 .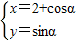 (α为参数)上任意一点,则(x-5)2+(y+4)2的最大值为 .
(α为参数)上任意一点,则(x-5)2+(y+4)2的最大值为 .
|
| A、6 | B、5 | C、36 | D、25 |
|
|
| y |
| x |
| ||
| 3 |
| ||
| 3 |
一、选择题: (每题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
小计
答案
D
D
B
C
C
C
B
C
A
C
二、填空题:本大题共4小题,每小题5分,共20分.
11. -5 12.7 13.(2,1) 14.例如:,分段函数也可(3分);=a/3.(2分)
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(12分)
已知:函数().解不等式:.
解:1)当时,即解,(2分)
即,(4分)不等式恒成立,即;(6分)
2)当时,即解(8分),即,(10分)因为,所以.(11分)
由1)、2)得,原不等式解集为.(12分)
16.(本小题满分12分)
解:1)
(2分) (4分)
(6分)
.(8分)
当时(9分),取最大值.(10分)
2)当时,,即,(11分)
解得,.(12分)
17.(本小题满分14分)
1)证明:连接AC.
∵点A是点P在底面AC上的射影,(1分)
∴PA^面AC.(2分)
PC在面AC上的射影是AC.
正方形ABCD中,BD^AC,(3分)
∴BD^PC.(4分)
2)解:连接OS.
∵BD^AC,BD^PC,
又AC、PC是面PAC上的两相交直线,
∴BD^面PAC. (6分)
∵OSÌ面PAC,
∴BD^OS.(7分)
正方形ABCD的边长为a,BD=,(8分)
∴DBSD的面积.(9分)
OS的两个端点中,O是定点,S是动点.
∴当取得最小值时,OS取得最小值,即OS^PC.(10分)
∵PC^BD, OS、BD是面BSD中两相交直线,
∴PC^面BSD.(12分)
又PCÌ面PCD,∴面BSD^面PCD.(13分)
∴面BSD与面PCD所成二面角的大小为90°.(14分)
18.(本小题满分14分)
1)解:设S(x,y),SA斜率=,SB斜率=,(2分)
由题意,得,(4分)
经整理,得.(6分,未指出x的范围,扣1分)
点S的轨迹C为双曲线(除去两顶点).(7分)
2)解:假设C上存在这样的两点P(x1,y1)和Q(x2,y2),则PQ直线斜率为-1,
且P、Q的中点在直线x-y-1=0上.
设PQ直线方程为:y=-x+b,
由整理得.(9分)
其中时,方程只有一个解,与假设不符.
当时,D>0,D=
=,
所以,(*)(10分)
又,所以,代入y=-x+b,
得,
因为P、Q中点在直线x-y-1=0上,
所以有:,整理得,(**)(11分)
解(*)和(**),得-1<b<0,0<t<1,(13分)
经检验,得:当t取(0,1)中任意一个值时,曲线C上均存在两点关于直线x-y-1=0对称.(14分)
19.(本小题满分14分)
解:甲选手胜乙选手的局数作为随机变量ξ,它的取值共有0、1、2、3四个值.
1)当ξ=0时,本场比赛共三局,甲选手连负三局,
P(ξ=0)=(1-0.6)3=0.064;(2分)
2)当ξ=1时,本场比赛共四局,甲选手负第四局,且前三局中,甲胜一局,
P(ξ=1)=;(4分)
3)当ξ=2时,本场比赛共五局,甲选手负第五局,且前四局中,甲胜二局,
P(ξ=2)=; (6分)
4)当ξ=3时,本场比赛共三局、或四局、或五局.其中共赛三局时,甲连胜这三局;共赛四局时,第四局甲胜,且前三局中甲胜两局;共赛五局时,第五局甲胜,且前四局中甲胜两局;
P(ξ=3)==0.68256(8分)
ξ的概率分布列为:
ξ
0
1
2
3
P
0.064
0.1152
0.13824
0.68256
(10分)
Eξ=0´P(ξ=0)+ 1´ P(ξ=1)+2´ P(ξ=2)+3´ P(ξ=3) (12分)
=0´0.064+1´0.1152+2´0.13824+3´0.68256=2.43926»2.4394.(14分)
20.(本小题满分14分)
解:(1)由题意知,(1分)
得,(3分)∴ (5分)
(2)(6分)
(8分)
(3)设存在S,P,r,(9分)
(10分)
即
(*) (12分)
因为s、p、r为偶数
1+2,(*)式产生矛盾.所以这样的三项不存在.(14分)
以上答案及评分标准仅供参考,如有其它解法请参照给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com