
题目列表(包括答案和解析)
已知方向向量为![]() 的直线
的直线![]() 过椭圆C:=1(a>b>0)的焦点以及点(0,
过椭圆C:=1(a>b>0)的焦点以及点(0,![]() ),椭圆C的中心关于直线
),椭圆C的中心关于直线![]() 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵过点E(-2,0)的直线![]() 交椭圆C于点M、N,且满足
交椭圆C于点M、N,且满足![]() ,(O为坐标原点),求直线
,(O为坐标原点),求直线![]() 的方程。
的方程。
已知方向向量为![]() 的直线l过点(
的直线l过点(![]() )和椭圆
)和椭圆![]() 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足![]() =
=![]() ,cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.
,cot∠MON≠0(O为原点).若存在,求直线m的方程;若不存在,请说明理由.

已知方向向量为![]() 的直线
的直线![]() 点
点![]() 和椭圆
和椭圆![]() 的焦点,且椭圆C的中心关于直线
的焦点,且椭圆C的中心关于直线![]() 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
(1)求椭圆C的方程
(2)是否存在过点![]() 的直线
的直线![]() 交椭圆C于点M,N且满足
交椭圆C于点M,N且满足
![]() (O为原点),若存在求出直线
(O为原点),若存在求出直线![]() 的方程,若不存在说明理由。
的方程,若不存在说明理由。
. 已知方向向量为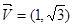 的直线l过椭圆
的直线l过椭圆 的焦点以及点(0,
的焦点以及点(0,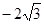 ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为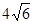 .
.
(1)求椭圆C的方程;
(2)过左焦点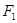 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, 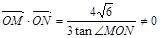 (O坐标原点),求直线m的方程.
(O坐标原点),求直线m的方程.
 的直线l过点
的直线l过点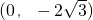 和椭圆
和椭圆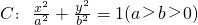 的右焦点,且椭圆的离心率为
的右焦点,且椭圆的离心率为 .
.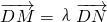 ,求实数λ的取值范围.
,求实数λ的取值范围.1.C 2.D 3.A 4.A 5.C 6.A 7.D 8.A 9.C 10.D 11.D12.B
13.2 14. 15.
15. 16.①③④
16.①③④
17. 
18.解:

⑴

 .
.
⑵在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
所以,当 时,
时, ;当
;当 时,
时, .
.
故 的值域为
的值域为 .
.
19.解:⑴直线 ①,
①,
过原点垂直于 的直线方程为
的直线方程为 ②
②
解①②得 ,
,
∵椭圆中心O(0,0)关于直线 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,
∴ ,
…………………(分)
,
…………………(分)
∵直线 过椭圆焦点,∴该焦点坐标为(2,0),
过椭圆焦点,∴该焦点坐标为(2,0),
∴ ,
,
故椭圆C的方程为 ③…………………12分)
③…………………12分)
20.点评:本小题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能,考查分析问题的能力和推理能力。
解:(Ⅰ)设这二次函数f(x)=ax2+bx (a≠0) ,则 f`(x)=2ax+b,由于f`(x)=6x-2,得
a=3 , b=-2, 所以 f(x)=3x2-2x.
又因为点 均在函数
均在函数 的图像上,所以
的图像上,所以 =3n2-2n.
=3n2-2n.
当n≥2时,an=Sn-Sn-1=(3n2-2n)-
=6n-5.
当n=1时,a1=S1=3×12-2=6×1-5,所以,an=6n-5 ( )
)
(Ⅱ)由(Ⅰ)
得知 =
= =
= ,
,
故Tn= =
=

= (1-
(1-
因此,要使 (1-
(1- )<
)< (
( )成立的m,必须且仅须满足
)成立的m,必须且仅须满足 ≤
≤ ,即m≥10,所以满足要求的最小正整数m为10.
,即m≥10,所以满足要求的最小正整数m为10.
21.(1)




(2)由
令 得,增区间为
得,增区间为 和
和 ,
,
减区间为








2

+
0
-
0
+


↑

↓

↑

由表可知:当 时,
时,

 解得:
解得:
 的取值范围为
的取值范围为
22.(1) 
(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com