题目列表(包括答案和解析)
（本小题满分12分）若规定一种对应关系
，使其满足：①
，且
；②如果
，那么
，
．现已知
，试求：
．
（本小题满分12分）
若(2x＋4)2010＝a0＋a1x＋a2x2＋…＋a2010x2010，则a0＋a2＋a4＋…＋a2010被3除的余数是多少?
（本小题满分12分）
若函数
为奇函数，当
时，
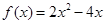（如图）．
（Ⅰ）求函数的表达式，并补齐函数的图象；
（Ⅱ）用定义证明：函数
在区间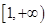
上单调递增．
（本小题满分12分）
若函数
的图象过
与
两点,设函数
;
（1）求
的定义域;
（2）求函数
的值域，判断g(x)奇偶性,并说明理由.
（本小题满分12分）
若函数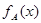
的定义域为
，其中a、b为任
意正实数，且a<b。
（1）当A=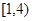
时，研究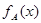的单调性（不必证明）；
（2）写出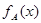的单调区间（不必证明），并求函数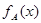的最小值、最大值；
（3）若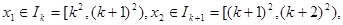
其中k是正整数，对一切正整数k不等式
都有解，求m的取值范围。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
A
D
B
C
C
A
B
C
B
A
13. 
14. 2 15. 
16. ① ④
17.1）
……2分
当
∴
……4分
，对称中心
……6分
（2）
……8分
……10分
，
……12分
18. 解：1）
……5分
（2）分布列：
0
1
2
3
4
，
，
，
评分：下面5个式子各1分，列表和期望计算2分（5＋2＝7分）
19. 解：（1）
所以
（2）设
……8分
当 
当
所以，当
的最小值为
……………………………… 12分
20.解法1：
（1）过S作
，
，连
∴
∴
……4分
（2）
，
，∴
是平行四边形
故平面
过A作
，
，连
∴
为平面
和
二面角平面角，而
应用等面积：
，
∵
，
故题中二面角为
……4分
（3）∵
∥，
到距离为
到距离
又∵
，
，∴
平面
，∴
平面
∴平面
平面
，只需B作SE连线BO1，BO1＝
设线面角为
，
，
，
∴
，故线面角为
……4分
解法2：
（1）同上
（2）建立直角坐标系
平面SDC法向量为
，
，
，
设平面SAD法向量
，取
，
，
∴
∴
∴二面角为
（3）设线面角为，
∴
21.（1）
时，
……
∴
∴
∴
（3分）
时，
……
∴
（5分）
故
（6分）
（2）
又∵
，∴
∴
（12分）
22.（1）设
，
，
∵
∴
，∴
（3分）
所以P点的轨迹是以
为焦点，实半轴长为1的双曲线的右支（除顶点）。（4分）
（2）设PE斜率为
，PR斜率为
PE：
PR：
令
，
，
∴
…………（6分）
由PF和园相切得：
，PR和园相切得：
故：
为
两解
故有：
，
……（8分）
又∵
，∴
，∴
（11分）
设
，
故
，
，
∴
（14分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com