一、选择题:本大题共12个小题,每小题5分,共60分。
1―5 BCBAB 6―10 DCCCD 11―12 DB
二、填空题:本大题共4个小题,每小题4分,共16分。
13. 14.
14. 15.1:2 16.①②⑤
15.1:2 16.①②⑤
20090203 17.(本小题满分12分) 解:(I) 共线 共线   ………………3分 ………………3分 故 …………6分 …………6分 (II)   …………12分 …………12分 18.(本小题满分12分) 解:根据题意得图02,其中BC=31千米,BD=20千米,CD=21千米, ∠CAB=60˚.设∠ACD = α ,∠CDB = β .

 , ,
 . .


 .……9分 .……9分
在△ACD中,由正弦定理得:  . .

19.(本小题满分12分) 解:(1)连结OP,∵Q为切点,PQ OQ, OQ, 由勾股定理有, 又由已知 即: 化简得 …………3分 …………3分 (2)由 ,得 ,得  …………6分 …………6分
故当 时, 时, 线段PQ长取最小值 线段PQ长取最小值 …………7分 …………7分 (3)设⊙P的半径为R,∵⊙P与⊙O有公共点,⊙O的半径为1, ∴ 即R 即R 且R 且R 而 故当 时, 时, ,此时b=―2a+3= ,此时b=―2a+3= 得半径最最小值时⊙P的方程为 …………12分 …………12分 20.(本小题满分12分) 解:(I)取PD的中点G,连结FG、AG,则

又E为AB的中点 
∴四边形AEFG为平行四边形 …………3分 ∴EF∥AG 又AG 平面PAD 平面PAD ∴EF∥平面PAD …………5分
(II)∵PA⊥平面ABCD ∴PA⊥AE 又矩形ABCD中AE⊥AD ∴AE⊥平面PAD ∴AE⊥AG ∴AE⊥EF 又AE//CD ∴ED⊥CD …………8分 又∵PA=AD ∴在Rt△PAE和Rt△CBE中PE=CE ∵D为PC的中点 ∴EF⊥PC …………10分 又PC∩CD=C ∴EF⊥平面PCD 又EF 平面PEC 平面PEC ∴平面PEC⊥平面PCD …………12分 22.(本小题满分12分) 解:(I)  单调递增。 …………2分 单调递增。 …………2分
① ,不等式无解; ,不等式无解; ② ; ; ③ ; ; 所以 …………6分 …………6分
(II) , …………8分 , …………8分 
……………11分 因为对一切 ……12分 ……12分 22.(本小题满分14分) 解:(I) 
(II) …………7分 …………7分 
(III)令 上是增函数 上是增函数 

| | | | | | | |

![]() 中,
中,![]() 是数列
是数列![]() 前
前![]() 项和,
项和,![]() ,当
,当![]()
![]() ;
;![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() ;
;![]() ,都有
,都有![]() 成立?若存在,求出m的最大值;若不存在,请说明理由。
成立?若存在,求出m的最大值;若不存在,请说明理由。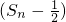 .
.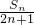 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; (m-8)成立?若存在,求出m的最大值;若不存在,请说明理由.
(m-8)成立?若存在,求出m的最大值;若不存在,请说明理由.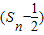 .
.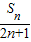 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; (m-8)成立?若存在,求出m的最大值;若不存在,请说明理由.
(m-8)成立?若存在,求出m的最大值;若不存在,请说明理由.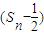 .
.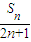 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn; (m-8)成立?若存在,求出m的最大值;若不存在,请说明理由.
(m-8)成立?若存在,求出m的最大值;若不存在,请说明理由. 14.
14. 15.1:2 16.①②⑤
15.1:2 16.①②⑤