
题目列表(包括答案和解析)
| 3 |
| 3 |
.如图是函数![]() 的图象,则其解析式是( )
的图象,则其解析式是( )
A.![]()
B.![]()
C.![]()
D. ![]()

C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.本小题满分15分)
如图,已知椭圆E: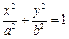
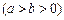 ,焦点为
,焦点为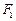 、
、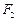 ,双曲线G:
,双曲线G: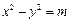
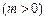 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设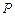 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线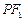 、
、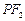 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形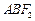 的周长等于
的周长等于 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为 .
.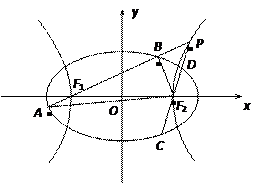
(1)求椭圆E与双曲线G的方程;
(2)设直线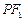 、
、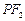 的斜率分别为
的斜率分别为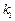 和
和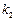 ,探求
,探求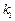 和
和
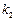 的关系;
的关系;
(3)是否存在常数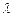 ,使得
,使得 恒成立?
恒成立?
若存在,试求出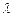 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.
.定义域为R的函数 满足
满足 ,且当
,且当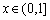 时,
时, ,则当
,则当 时,
时,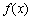 的最小值为( )
的最小值为( )
(A) (B)
(B)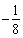 (C)
(C)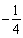 (D)
(D)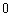
一、选择题:本大题主要考查基本知识和基本运算.共12小题,每小题5分,满分60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
B
A
B
C
D
C
B
D
C
C
二、填空题:本大题主要考查基本知识和基本运算.本大题共4小题,每小题4分,满分16
分.13. 14.
14. 15.
15. 16.
16. 或
或
三、解答题:本大题共6小题,满分74分.解答须写出文字说明、证明过程和演算步骤.
17.(本小题满分12分)
解:(1)∵
 …… 2分
…… 2分
 …… 4分
…… 4分
 .
…… 6分
.
…… 6分
∴ .
…… 8分
.
…… 8分
(2) 当 时,
时,  取得最大值, 其值为2 .
……10分
取得最大值, 其值为2 .
……10分
此时 ,即
,即
 Z
Z .
……12分
.
……12分
18. (本小题满分12分)
解:(1) 由频率分布条形图知,抽取的学生总数为 人.
……4分
人.
……4分
∵各班被抽取的学生人数成等差数列,设其公差为 ,
,
由 =100,解得
=100,解得 .
.
∴各班被抽取的 学生人数分别是22人,24人,26人,28人. ……8分
学生人数分别是22人,24人,26人,28人. ……8分
(2) 在抽取的学生中,任取一名学生, 则分数不小于90分的概率为0.35+0.25+0.1+0.05=0.75.……12分
19.(本小题满分14分)解:(1)∵  ⊥平面
⊥平面 ,
,
 平面
平面 ,
,
∴
 ⊥
⊥ .
…… 2分
.
…… 2分
∵
 ⊥
⊥ ,
,


 ,
,
∴
 ⊥平面
⊥平面 ,
…… 4分
,
…… 4分
∵ 
 平面
平面 ,∴
,∴  ⊥
⊥ .
…… 6分
.
…… 6分
 (2)法1: 取线段
(2)法1: 取线段 的中点
的中点 ,
, 的中点
的中点 ,连结
,连结 ,
,
则 是△
是△ 中位线.
中位线.
∴ ∥
∥ ,
, ,
……8分
,
……8分
∵
 ,
, ,
,
∴ .
.
∴
四边形 是平行四边形,
……10分
是平行四边形,
……10分
∴  .
.
∵ 
 平面
平面 ,
,
 平面
平面 ,
,
∴  ∥平面
∥平面 .
.
∴
线段 的中点
的中点 是符合题意要求的点.
……12分
是符合题意要求的点.
……12分
法2: 取线段 的中点
的中点 ,
, 的中点
的中点 ,连结
,连结 ,
,
 则
则 是△
是△ 的中位线.
的中位线.
∴ ∥
∥ ,
, ,
,
∵ 平面
平面 ,
,  平面
平面 ,
,
∴ 平面
平面 .
…… 8分
.
…… 8分
∵
 ,
, ,
,
∴ .∴ 四边形
.∴ 四边形 是平行四边形,
是平行四边形,
∴  ∵
∵ 
 平面
平面 ,
,
 平面
平面 ,
,
∴  ∥平面
∥平面 .
……10分
.
……10分
∵ ,∴平面
,∴平面 平面
平面 .∵
.∵ 平面
平面 ,
,
∴ ∥平面
∥平面 .
.
∴
线段 的中点
的中点 是符合题意要求的点.
……12分
是符合题意要求的点.
……12分
20、(本小题满分12分)
解:解:(1)
 ①式 …………1分
①式 …………1分
 …………3分
…………3分
由条件 ②式…………5分
②式…………5分
由①②式解得
(2) ,
,
令 …………8分
…………8分
经检验知函数 ,
,
 的取值范围。 …………12分
的取值范围。 …………12分
21. (本小题满分12分)
(1) 解:当 时,
时, .
……1分
.
……1分
当 时,
时,

 .
……3分
.
……3分
∵ 不适合上式,
不适合上式,
∴ ……4分
……4分
(2)证明: ∵ .
.
当 时,
时, ……6分
……6分
当 时,
时, , ①
, ①
 . ②
. ②
①-②得:


得 ,
……8分
,
……8分
此式当 时也适合.
时也适合.
∴ N
N .
∵
.
∵ ,∴
,∴ .
……10分
.
……10分
当 时,
时, ,
,
∴ .
∵
.
∵ ,∴
,∴ .
故
.
故 ,即
,即 .
.
综上, .
……12分
.
……12分
22. (本小题满分14分)
解:(1)依题意知, …… 2分
…… 2分
∵ ,
, .
…… 4分
.
…… 4分
∴所求椭圆 的方程为
的方程为 .
…… 6分
.
…… 6分
(2)∵ 点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
∴  …… 8分
…… 8分
解得: ,
, .
…… 10分
.
…… 10分
∴ .
…… 12分
.
…… 12分
∵ 点
 在椭圆
在椭圆 :
: 上,∴
上,∴ , 则
, 则 .
.
∴ 的取值范围为
的取值范围为 .
……14分
.
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com