
题目列表(包括答案和解析)
..如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(1)设 (单位:米),要使花
(单位:米),要使花 坛AMPN的面积大于32平方米,求
坛AMPN的面积大于32平方米,求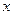 的取值范围;
的取值范围;
|
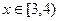 (单位:米),则当AM,A
(单位:米),则当AM,A N的长度分别是多少
N的长度分别是多少 时,花坛AMPN的面积最大?并求出最大面积。
时,花坛AMPN的面积最大?并求出最大面积。 ..(本小题满分12分)
已知: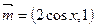 ,
,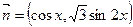 ,
,
函数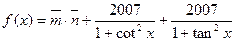 .
.
(1)化简 的解析式,并求函数的单调递减区间;
的解析式,并求函数的单调递减区间;
(2)在△ABC中,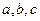 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知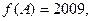
 ,△ABC的面积为
,△ABC的面积为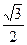 ,求
,求 的值.
的值.
..在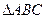 中,
中, 分别为内角
分别为内角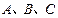 所对的边,且
所对的边,且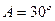 .
.
现给出三个条件:①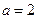 ; ②
; ②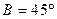 ;③
;③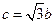 .试从中选出两个可以确定
.试从中选出两个可以确定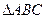 的条件,并以此为依据求
的条件,并以此为依据求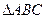 的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的 的面积为
的面积为
..(满分8分)已知数列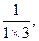
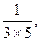
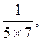

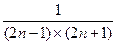 ,
,
(1)计算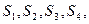
(2)根据(1)的计算结果,猜想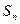 的表达式
的表达式 ,并用数学归纳法进行证明。
,并用数学归纳法进行证明。
..(本小题满分12分)
数列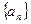 的各项均为正数,
的各项均为正数, 为其前
为其前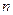 项和,对于任意
项和,对于任意 ,总有
,总有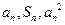 成等差数列.
成等差数列.
(1)求数列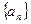 的通项公式;
的通项公式;
(2)设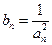 ,数列
,数列 的前
的前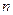 项和为
项和为 ,求证:
,求证: .
.
一、选择题 CAADD ABDAB CB
二、填空题  .
.
 .
.
 .
.
 .
.
三、解答题
 .
.




 的周期为
的周期为 ,最大值为
,最大值为 .
.
 令
令 ,
,
得 ,
, .
.
∴ 的单调减区间为
的单调减区间为
 .
.
 .
. 事件
事件 ,
, 表示甲以
表示甲以 获胜;
获胜; 表示乙以
表示乙以 获胜,
获胜, 、
、 互斥,
互斥,
∴
 .
.
 事件
事件 ,
, 表示甲以
表示甲以 获胜;
获胜; 表示甲以
表示甲以 获胜,
获胜,  、
、 互斥,
互斥,
∴

 延长
延长 、
、 交于
交于 ,则
,则 .
.
连结 ,并延长交
,并延长交 延长线于
延长线于 ,则
,则 ,
, ,
,
 在
在 中,
中, 为中位线,
为中位线, ,
,
又 ,
,
∴ .
.
 ∵
∵ 中,
中, ,
,
∴ .
.
即 ,又
,又 ,
, ,
,
∴ ,∴
,∴ ,
,
∴ 为平面
为平面 与平面
与平面 所成二面角的平面角。
所成二面角的平面角。
又 ,
,
∴所求二面角大小为 .
.
 .
. 由
由 ,
, ,
,
知 ,
, ,同理
,同理 ,
, .
.
又 ,
,
∴ 构成以
构成以 为首项,以
为首项,以 为公比的等比数列。
为公比的等比数列。
∴ ,即
,即 .
.





 .
.
 .
.
 ,且
,且 的图象经过点
的图象经过点 和
和 ,
,
∴ ,
, 为
为 的两根.
的两根.
∴

∴
由
解 得
得
∴
 要使对
要使对 ,不等式
,不等式 恒成立,
恒成立,
只需 即可.
即可.
∵ ,
,
∴ 在
在 上单调递减,在
上单调递减,在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
又 ,
, ,
,
∴ ,
,
∴ ,
,
解得 ,即为
,即为 的取值范围.
的取值范围.
 .
. 由题意知,椭圆
由题意知,椭圆 的焦点
的焦点 ,
, ,顶点
,顶点 ,
, ,
,
∴双曲线 中
中 ,
, ,
, .
.
∴ 的方程为:
的方程为: .
.
 联立
联立 ,得
,得 ,
,
∴
 且
且 ,
,
设 ,
, ,
,
则 ,
,
∴ .
.
又 ,即
,即 ,
,
∴ ,
,
即 .
.
∴ ,
,
 ,
,
由①②得 的范围为
的范围为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com