
题目列表(包括答案和解析)
5名工人独立地工作,假定每名工人在1小时内平均12分钟需要电力(即任一时刻需要电力的概率为12/60)
(1)设X为某一时刻需要电力的工人数,求 X的分布列及期望;
(2)如果同一时刻最多能提供3名工人需要的电力,求电力超负荷的概率,并解释实际意义.
.(本小题满分13分)汽车和自行车分别从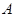 地和
地和 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知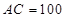 米.(汽车开到
米.(汽车开到 地即停止)
地即停止)

(Ⅰ)经过 秒后,汽车到达
秒后,汽车到达 处,自行车到达
处,自行车到达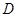 处,设
处,设 间距离为
间距离为 ,试
,试
写出 关于
关于 的函数关系式,并求其定义域.
的函数关系式,并求其定义域.
(Ⅱ)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
(14分)某养殖厂需定期购买饲料,已知该厂每天需要饲料200公斤,每公斤饲料的价格为1.8元,饲料的保管与其他费用为平均每公斤每天0.03元,购买饲料每次支付运费300元.
(Ⅰ)求该厂多少天购买一次饲料才能使平均每天支付的总费用最小;
(Ⅱ)若提供饲料的公司规定,当一次购买饲料不少5吨时其价格可享受八五折优惠(即原价的85%).问该厂是否考虑利用此优惠条件,请说明理由.
(10分)在一次国际大型体育运动会上,某运动员报名参加了其中5个项目的比赛.已知该运动员在这5个项目中,每个项目能打破世界纪录的概率都是0.8,那么在本次运动会上:
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为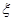 ,求
,求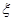 的数学期望
的数学期望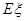 (即均值).
(即均值).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com