
题目列表(包括答案和解析)
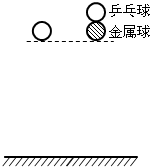 把一只乒乓球从胸前的某个高度释放,落到坚硬的水泥地上,反弹后可以达到接近胸前释放时的高度,但无论如何是不会超过这个高度的.同样取一只刚性很好的金属球,从相同高度释放,反弹后也不会跳得更高,这是由能量守恒定律决定的.如果如图所示那样,把乒乓球放在金属球上面,让它们从原来高度落下,落地反弹以后,乒乓球会跳多高呢?也许你会感到吃惊,乒乓球比单独下落跳得更高.这就是著名的超级球问题!
把一只乒乓球从胸前的某个高度释放,落到坚硬的水泥地上,反弹后可以达到接近胸前释放时的高度,但无论如何是不会超过这个高度的.同样取一只刚性很好的金属球,从相同高度释放,反弹后也不会跳得更高,这是由能量守恒定律决定的.如果如图所示那样,把乒乓球放在金属球上面,让它们从原来高度落下,落地反弹以后,乒乓球会跳多高呢?也许你会感到吃惊,乒乓球比单独下落跳得更高.这就是著名的超级球问题!【解析】(1)电动机的输出功率为![]() W
W
F安=BIL=![]()
当速度稳定时,由平衡条件得![]()
解得v=2m/s
(2)由能量守恒定律得 ![]()
解得t=1s
解析 (1)设木板第一次上升过程中,物块的加速度为a物块,由牛顿第二定律kmgsin θ-mgsin θ=ma物块
解得a物块=(k-1)gsin θ,方向沿斜面向上
(2)设以地面为零势能面,木板第一次与挡板碰撞时的速度大小为v1
由机械能守恒得:![]() ×2mv
×2mv![]() =2mgH
=2mgH
解得v1=![]()
设木板弹起后的加速度为a板,由牛顿第二定律得:
a板=-(k+1)gsin θ
木板第一次弹起的最大路程s1=![]() =
=![]()
木板运动的路程s=![]() +2s1=
+2s1=![]()
(3)设物块相对木板滑动距离为L
根据能量守恒mgH+mg(H+Lsin θ)=kmgLsin θ
摩擦力对木板及物块做的总功W=-kmgLsin θ
解得W=-![]()
答案 (1)(k-1)gsin θ;方向沿斜面向上
(2)![]() (3)-
(3)-![]()
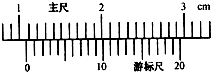 (1)通常用的游标卡尺,在游标上有20个小等分刻度,它们的总长度为19mm,它的每一分度与主尺的最小分度1mm相差
(1)通常用的游标卡尺,在游标上有20个小等分刻度,它们的总长度为19mm,它的每一分度与主尺的最小分度1mm相差| 1 |
| 20 |

| 时刻 | t2 | t3 | t4 | t5 |
| 速度(m/s) | 4.99 | 4.48 | 3.98 | ? |
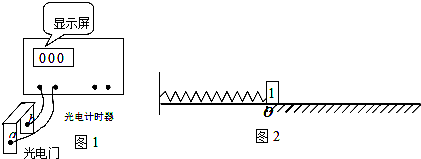
| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 压缩量x/cm | 10 | 15 | 20 | 25 | 30 | 35 |
| 时间t/s | 0.100 | 0.067 | 0.050 | 0.040 | 0.033 | 0.029 |
| 距离s/m | 0.50 | 1.13 | 2.00 | 3.12 | 4.50 | 6.13 |
| L |
| t |
| L |
| t |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com