练习册

  • 练习册
  • 试题
    (3)发生一系列碰撞后.直到最后第n个木块到达底端.在整个过程中.由于碰撞所损失的总机械能总. 北 京 西 城 区 抽 样 测 试 【查看更多】

     

    题目列表(包括答案和解析)

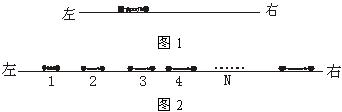
    20. （1）如图1，在光滑水平长直轨道上，放着一个静止的弹簧振子，它由一轻弹簧两端各联结一个小球构成，两小球质量相等.现突然给左端小球一个向右的速度v0，求弹簧第一次恢复到自然长度时，每个小球的速度.

    （2）如图2，将N个这样的振子放在该轨道上，最左边的振子1被压缩至弹簧为某一长度后锁定，静止在适当位置上，这时它的弹性势能为E0，其余各振子间都有一定的距离.现解除对振子1的锁定，任其自由运动，当它第一次恢复到自然长度时，刚好与振子2碰撞，此后，继续发生一系列碰撞，每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后，每个振子弹性势能的最大值.已知本题中两球发生碰撞时，速度交换，即一球碰后的速度等于另一球碰前的速度.

    查看答案和解析>>

    （1）如图6-15，在光滑水平长直轨道上，放着一个静止的弹簧振子，它由一轻弹簧两端各连接一个小球构成，两小球质量相等.现突然给左端小球一个向右的速度u0，求弹簧第一次恢复到自然长度时，每个小球的速度.

    图6-15

    （2）如图6-16，将N个这样的振子放在该轨道上，最左边的振子1被压缩至弹簧为某一长度后锁定，静止在适当位置上，这时它的弹性势能为E0.其余各振子间都有一定的距离，现解除对振子1的锁定，任其自由运动，当它第一次恢复到自然长度时，刚好与振子2碰撞，此后，继续发生一系列碰撞，每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰.求所有可能的碰撞都发生后，每个振子弹性势能的最大值.已知本题中两球发生碰撞时，速度交换，即一球碰后的速度等于另一球碰前的速度.

    图6-16

    查看答案和解析>>

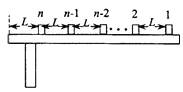
    如图所示，n个相同的木块（视为质点），每块的质量都是m，从右向左沿同一直线排列在水平桌面上，相邻木块间的距离均为L，第n个木块到桌边缘的距离也是L，木块与桌面间的摩擦系数为μ. 开始时，第1个木块以初速度v0向左滑行，其余所有木块都静止，在每次碰撞后，发生碰撞的木块都粘在一起运动. 最后第n个木块刚好滑到桌边而没有掉下.

       （1）求在整个过程中损失的机械能和因碰撞而损失的总动能；

       （2）求第i次（i≤n－1）碰撞中损失的动能与碰撞前动能之比？

       （3）若n=4，L=0.1m，v0=3m/s，取g=10m/s2，求μ的数值.

                                

    查看答案和解析>>

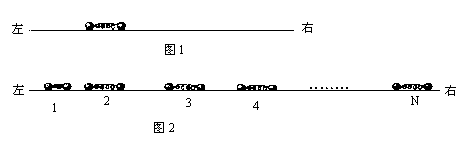
    (1)如图1，在光滑水平长直轨道上，放着一个静止的弹簧振子，它由一轻弹簧两端各联结一个小球构成，两小球质量相等，现突然给左端小球一个向右的速度u0，求弹簧第一次恢复到自然长度时，每个小球的速度．

    (2)如图2，将N个这样的振子放在该轨道上，最左边的振子1被压缩至弹簧为某一长度后锁定，静止在适当位置上，这时它的弹性势能为E0，其余各振子间都有一定的距离．现解除对振子1的锁定，任其自由运动，当它第一次恢复到自然长度时，刚好与振子2碰撞，此后，继续发生一系列碰撞，每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰．求所有可能的碰撞都发生后，每个振子弹性势能的最大值．已知本题中两球发生碰撞时，速度交换，即一球碰后的速度等于另一球碰前的速度．

    查看答案和解析>>

    (1)如图甲，在光滑水平长直轨道上，放着一个静止的弹簧振子，它由一轻弹簧两端各连接一个小球构成，两小球质量相等．现突然给左端小球一个向右的速度u0，求弹簧第一次恢复到自然长度时，每个小球的速度．

    (2)如图乙，将N个这样的振子放在该轨道上．最左边的振子1被压缩至弹簧为某一长度后锁定，静止在适当位置上，这时它的弹性势能为E0．其余各振子间都有一定的距离．现解除对振子1的锁定，任其自由运动，当它第一次恢复到自然长度时，刚好与振子2碰撞，此后，继续发生一系列碰撞，每个振子被碰后刚好都是在弹簧第一次恢复到自然长度时与下一个振子相碰．求所有可能的碰撞都发生后，每个振子弹性势能的最大值．已知本题中两球发生碰撞时，速度交换，即一球碰后的速度等于另一球碰前的速度．

    查看答案和解析>>

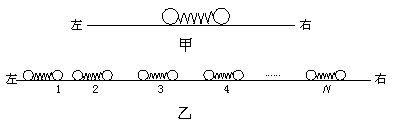
    第Ⅰ卷：选择正确答案（每小题3分共48分）

    (11~16题，全部选对得3分，选不全得1分，有选错或不答的得0分．)

    1．C  2．A   3．D  4．B   5．D   6．C  7．A   8．C   9．B   10．D

    11．AB   12．ABD   13．BC    14．AD   15．BCD   16．ABD

    第Ⅱ卷：计算题（共5题，52分）（不同解法，只要正确同样相应给分。）

    17．（9分）

    解：（1）物体受力如右图所示                　　　　 （1分）

    由牛顿运动定律　　　mgsinθ －μN = ma  　　 （1分）

    　　　　　　　　　　　　　　N － mgcosθ = 0　　 　 （1分）

    解得            a = gsinθ －μgcosθ = 3.6m/s2   （1分）

        （2） 由　           　　　　　　       （1分）

                求出　　　　　　　　　           　（1分）

    （3）由匀变速直线运动规律　          （1分）

    由牛顿第二定律　　               （1分）

    解得　　         　　　　 　     　（1分）

    18．（9分）

    解：（1）万有引力提供向心力   （2分）

    求出                        （1分）

       （2）月球表面万有引力等于重力      （2分）

       求出                       （1分）

    （3）根据                       （2分）

      求出                         （1分）

    19．（10分）

    解：（1）根据法拉第电磁感应定律    （3分） 

        求出        E = 1.2（V）                   （1分）

    （2）根据全电路欧姆定律   （1分）

            根据                               （1分）

        求出        P = 5.76×10-2（W）             （1分）

    （3）S断开后，流经R2的电量即为S闭合时C板上所带的电量Q

    电容器两端的电压     U = IR2＝0.6（V）     （1分）

    流经R2的电量    Q = CU = 1.8×10-5（C）    （2分）

    20．（12分）粒子的运动轨迹如右图所示   （1分）

    （1）设粒子在电场中运动的时间为t1

             x、y方向   2h = v0t1      （2分）

          根据牛顿第二定律   Eq = ma     （1分）

          求出                  （1分）

    （2）根据动能定理   （1分）

    设粒子进入磁场时速度为v，根据 （1分）

         求出                          （1分）

    （3）粒子在电场中运动的时间            （1分）

           粒子在磁场中运动的周期     （1分）

    设粒子在磁场中运动的时间为t2        （1分）

    求出                （1分）

    21．（12分）

    解：（1）设小木块1碰前的速度为v1，从开始运动到碰前，根据动能定理

                         （2分）

    　　　　对小木块1和2，由动量守恒    mv1 = 2mv           （1分）

            求出　　             （1分）

    （2）碰撞前损失的机械能为   1 = μmgcosθ?l          （1分）

         因碰撞损失的机械能为         （1分）

         求出    （1分）

    （3）对n个木块碰撞的全过程

    重力做的总功（1分）

    克服摩擦做的总功

          （1分）

    根据功与能的关系                  （2分）

    由以上各式求出    （1分

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     


    同步练习册答案