如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P₁（-a，b）点以相同的速率v₀在：xoy平面内朝x轴上方的各个方向射出（即0＜θ≤π），不计重力及粒子间的相互作用，且已知a足够大．
（1）试在图（甲）中的适当位置和区域加一垂直于xoy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
（2）试在图（乙）中的某些区域加垂直于xoy平面、磁感应强度为B的匀强磁场，使从P₁点发出的这簇带电粒子通过磁场后都能通过P₂（a，b）点．要求：
①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示v₀方向射出的带电粒子运动的轨迹；
③写出所加磁场区域与xoy平面所成截面边界的轨迹方程．

查看答案和解析>>

查看答案和解析>>

如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P₁（-a，0）点以相同的速率v_o在xOy平面内朝x轴上方的各个方向射出（即0＜θ≤π），不计重力及粒子间的相互作用，且已知a足够大．
（1）试在图中的适当位置和区域加一垂直于xOy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
（2）试在图中的某些区域再加垂直于xOy平面、磁感应强度为B的匀强磁场，使从Pl点发出的这簇带电粒子通过磁场后都能通过P₂（a，0）点．
要求：①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示v_o方向射出的带电粒子运动的轨迹；
③写出所加磁场区域与xOy平面所成截面边界的轨迹方程．

查看答案和解析>>

如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P₁（-a，b）点以相同的速率v₀在：xoy平面内朝x轴上方的各个方向射出（即0＜θ≤π），不计重力及粒子间的相互作用，且已知a足够大．
（1）试在图（甲）中的适当位置和区域加一垂直于xoy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
（2）试在图（乙）中的某些区域加垂直于xoy平面、磁感应强度为B的匀强磁场，使从P₁点发出的这簇带电粒子通过磁场后都能通过P₂（a，b）点．要求：
①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示v₀方向射出的带电粒子运动的轨迹；
③写出所加磁场区域与xoy平面所成截面边界的轨迹方程．

查看答案和解析>>

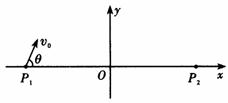
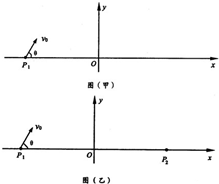如图所示，质量均为m、电荷量均为q的带负电的一簇粒子从P₁(一a，0)点以相同的速率v_o在xOy平面内朝x轴上方的各个方向射出(即0<θ≤π)，不计重力及粒子间的相互作用，且已知a足够大．
    (1)试在图中的适当位置和区域加一垂直于xOy平面、磁感应强度为B的匀强磁场，使这簇带电粒子通过该磁场后都沿平行于x轴方向运动．在图中定性画出所加的最小磁场区域边界的形状和位置．
    (2)试在图中的某些区域再加垂直于xOy平面、磁感应强度为B的匀强磁场，使从Pl点发出的这簇带电粒子通过磁场后都能通过P₂(a，0)点．
要求：①说明所加磁场的方向，并在图中定性画出所加的最小磁场区域边界的形状和位置；
②定性画出沿图示v_o方向射出的带电粒子运动的轨迹；
 
③写出所加磁场区域与xOy平面所成截面边界的轨迹方程．

查看答案和解析>>

选择题

1

2

3

4

5

6

7

8

9

B

D

D

C

A

BC

ABC

BC

AD

三、简答题：

10、正、反、10000

11、（1）并联电阻箱后线路总电阻减小，从而造成总电流增大。

   （2）① 调节电阻箱R，断开开关K，将开关S接D，记录电阻箱的阻值和电流表示数；                  

②断开开关K，再调节电阻箱R，将开关S接D，记录电阻箱的阻值和电流表示数；

（3）2.85；2.37

12、AD　　          １３、ＢＤ

四、计算题：

14、解：根据题意，当B与C刚脱离接触的瞬间，C的水平速度达到最大，水平方向的加速度

为零，即水平方向的合外力为零．由于小球此时仅受重力和杆子作用力，而重力是竖直向下的，

所以杆子的作用力必为零．列以下方程：

mgsinθ=mv²/L，(3分)

v_x＝vsinθ，(2分)

v_c＝v_x，(1分)

mgL(1―sinθ)=mv²/2+Mv_c²/2(1分)

解以上各式得m/M＝1/4(4分)

15．解：(1)由v-t图可知道，刚开始，t＝0时刻．线圈加速度为a＝v₀/t₁?

  此时感应电动势ε=ΔФ/Δt=ΔBL²/Δt，I=ε/R=ΔBL²/(ΔtR)

  线圈此刻所受安培力为F＝BIL＝BΔBL³/(ΔtR)＝ma，得到ΔB/Δt＝mv₀R/(B₀t₁L³)

  (2)线圈t₂时刻开始做匀速直线运动，有两种可能：

  a．线圈没有完全进入磁场，磁场就消失，所以没有感应电流，回路电功率P＝0．(3分)

  b．磁场没有消失，但线圈完全进入磁场，尽管有感应电流．所受合力为零，同样做匀速直线运动P=ε²/R=(2ΔBL²/Δt)²/R=4m²v²₀R/(B₀²t₁²L²)

16．解：(1)开始砂轮给铁板向前的滑动摩擦力F₁＝μ₁F_lN＝0．3X100N＝30N．

    工作台给平板的摩擦阻力F₂＝μ₂F_2N＝0．1X(100+l0X10)N＝20N．

    铁板先向右做匀加速直线运动a=(F₁-F₂)/m=1m/s²

加速过程铁板达到的最大速度v_m=ωR=5X0．4m／s＝2m／s．

    这一过程铁板的位移S_l＝v_m/2a=2m<2．8m

    此后砂轮给铁板的摩擦力将变为静摩擦力F_l^，，F_l’＝F₂，铁板将做匀速运动．

    即整个过程中铁板将先做加速度a＝lm／s²的匀加速运动，然后做v_m＝2m／s的匀速运动(只要上面已求出，不说数据也得分)(7分)

    (2)在加速运动过程中，由v_m=at₁得t₁＝2s，

    匀速运动过程的位移为s₂＝L―s₁＝0．8m由s₂＝vt₂，得t₂＝0．4s．

    所以加工一块铁板所用的时间为T＝t₁+t₂＝2．4s．(4分)

    (3)E＝ΔE_k+Q₁+Q₂＝136J．(4分)

    17．(15分)解：(1)设带电粒子从A点离开磁场区域，A点坐标为(x、y)，粒子旋转的半径为R，旋转的圆心在C点，旋转圆心角为α，则x＝一a+Rsinα，y= R―Rcosα，(4分)

    解得(x+a)²+(y一R)²＝R²．(2分)

  可见，所加磁场的边界的轨迹是一个以(一a，R)为圆心，半径为R＝mVo／Bq的圆．该圆位于x轴上方且与P₁点相切．(1分)

    (2)根据对称性可得出在P₂处所加的磁场最小区域也是圆，(1分)

    同理可求得其方程为(x-a)²+(y一R)²＝R² (2分)

圆心为(a，R)，半径为R＝mVo／Bq，该圆位于x轴上方且与P₂点相切；(2分)  

    根据左手定则判断，磁场方向垂直于xOy平面向里；(1分)

    沿图示v₀方向射出的带电粒子运动的轨迹如图所示．(2分)