20081125
解得 (2分)
(2分)
②在该星球表面上小球所受万有引力为
 (2分)
(2分)
(1分).
(2) ①从B到C的过程中,加速度大小为a1==2 m/s2 (2分),
又a1=mg,所以m=0.2
(2分),
②从A到B的过程中,加速度大小为a2
根据牛顿第二定律 mgsinq-mmgcosq=ma2 (2分),
a2=4.4 m/s2
a2==4.4 m/s2
(2分),
VA=2.0 m/s
(1分)
18(16分)
解:设导体杆切割磁感线产生的感应电动势为E,感应电流为I。外电路为ad、dc、cb三边电阻串联后再与ab边电阻并联,设总电阻为R,ab边和dc边的电流分别为Iab和Idc。
⑴ 金属框受重力和安培力,处于静止状态,有:
 (3分)
(3分)
 (2分)
(2分)
 =7.5A
(3分)
=7.5A
(3分)
⑵ E=B1L1 (3分)
(3分)
E=IR , , (2分)
, (2分)
得:  (3分)
(3分)
19题(17分)
(1)由动能定理: (
2分)
(
2分)
n价正离子在a、b间的加速度 ( 1分)
( 1分)
在a、b间运动的时间 =
= d
(
2分)
d
(
2分)
在MN间运动的时间:t2=L/v
(
1分)
离子到达探测器的时间:
t=t1+t2= (
2分)
(
2分)
(2)假定n价正离子在磁场中向N板偏转,洛仑兹力充当向心力,设轨迹半径为R,由牛顿第二定律得: ( 2分)
( 2分)
离子刚好从N板右侧边缘穿出时,由几何关系:
R2=L2+(R-L/2)2
(2分)
由以上各式得: ( 2分)
( 2分)
当n=1时U1取最小值
 (
3分)
(
3分)
20.(17分)
(1)设A在C板上滑动时,B相对于C板不动,据题意对B、C分析有:
μmg=2ma,得 ,
( 1分)
,
( 1分)
又B最大的加速度为 由于am>a,所以B相对于C不滑动而一起向右做匀加速运动,则
由于am>a,所以B相对于C不滑动而一起向右做匀加速运动,则 。
(
2分)
。
(
2分)
(2)若物块A刚好与物块B发生碰撞,则A相对于C运动到B所在处时,A、B的速度大小相等,因为B与木板C的速度相等,所以此时三者的速度均相同,设为v1,由动量守恒定律得:
 mv0=3mv1 ①
(
2分)
mv0=3mv1 ①
(
2分)
在此过程中,设木板C运动的路程为s1,则A运动的路程为s1+L,如图所示,由动能定理得
对B、C系统有 ②
( 2分)
②
( 2分)
对A有 ③ (2分)
③ (2分)
联立①、②、③解得: ,欲使A与B发生碰撞,须满足
,欲使A与B发生碰撞,须满足
 ( 2分)
( 2分)
设B刚好不滑离木板C,此时三者的共同速度为v2,同理得
mv0=3mv2
④ (2分)
在此过程中,A、B、C系统克服滑动摩擦力做功,减少的机械能转化为系统的内能,由能的转化和守恒得  ⑤ ( 2分)
⑤ ( 2分)
联立④、⑤解得
综上所述,使物块A能与B发生碰撞,而B又不滑离C,则物块A的初速度v0应满足
 。
(2分)
。
(2分)


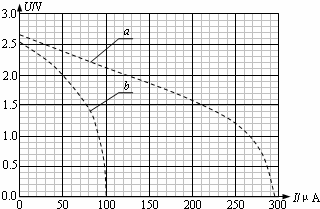


 ×10
×10  (3分)
(3分) (1) 连接电路如答案图(5分)
(2) A (2分) (3) 1.6×
(1) 连接电路如答案图(5分)
(2) A (2分) (3) 1.6× ,
,