练习册

  • 练习册
  • 试题
    16．如图所示.两条平行的足够长的光滑金属导轨与水平面成=37o角.导轨间距离L=0.6 m.其上端接一电容和一固定电阻.电容C＝10mF.固定电阻 R＝4.5 W.导体棒ab与导轨垂直且水平.其质量m＝3×10-2kg.电阻r＝0.5W.整个装置处于垂直导轨平面向上的匀强磁场中.已知磁感应强度B＝0.5T.取g＝10 m/s2.sin 37o＝ 0.8.cos 37o＝0.6.现将ab棒由静止释放.当它下滑的速度达到稳定时.求:(1) 此时通过ab棒的电流,(2) ab棒的速度大小,(3) 电容C与a端相连的极板所带的电荷量. 【查看更多】

     

    题目列表(包括答案和解析)

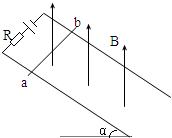    精英家教网如图所示，两条平行的足够长的光滑金属导轨与水平面成α=53°角，导轨间距离L=0.8m．其上端接一电源和一固定电阻，电源的电动势E=1.5V，其内阻及导轨的电阻可忽略不计．固定电阻R=4.5Ω．导体棒ab与导轨垂直且水平，其质量m=3×10-2kg，电阻不计．整个装置处于竖直向上的匀强磁场中，磁感应强度B=0.5T．（g=10m/s2  sin53°=0.8  cos53°=0.6 ）
    （1）将ab棒由静止释放，最终达到一个稳定的速度，求此时电路中的电流．
    （2）求ab稳定时的速度．
    （3）求ab棒以稳定速度运动时电路中产生的焦耳热功率PQ及ab棒重力的功率PG．
    从计算结果看两者大小关系是怎样的？请解释为什么有这样的关系？

    查看答案和解析>>

    如图所示，两条平行的足够长的光滑金属导轨与水平面成α=53??角，导轨间距离L=0.8m.其上端接一电源和一固定电阻，电源的电动势E=1.5V,其内阻及导轨的电阻可忽略不计. 固定电阻R=4.5Ω.导体棒ab与导轨垂直且水平，其质量m=3×10-2kg,电阻不计. 整个装置处于竖直向上的匀强磁场中，磁感应强度B=0.5T.(g=10m/s2  sin53??=0.8  cos53??=0.6 )

    （1）将ab棒由静止释放，最终达到一个稳定的速度，求此时电路中的电流；

    （2）求ab稳定时的速度；

    （3）求ab棒以稳定速度运动时电路中产生的焦耳热功率PQ及ab棒重力的功率PG .

       从计算结果看两者大小关系是怎样的？请解释为什么有这样的关系？

    查看答案和解析>>

    如图所示，两条平行的足够长的光滑金属导轨与水平面成=37o角，导轨间距离L=0.6 m，其上端接一电容和一固定电阻，电容C＝10F，固定电阻??。导体棒ab与导轨垂直且水平，其质量m＝3×10－2kg，电阻r＝0.5。整个装置处于垂直导轨平面向上的匀强磁场中，已知磁感应强度B＝0.5T，取g＝10 m/s2，sin 37o＝0.6，cos 37o＝0.8。现将ab棒由静止释放，当它下滑的速度达到稳定时，求：

    (1)  此时通过ab棒的电流；

    (2)  ab棒的速度大小；

    (3) 电容C与a端相连的极板所带的电荷量。 

    查看答案和解析>>

    如图所示，两条平行的足够长的光滑金属导轨与水平面成α=53º角，导轨间距离L=0.8m.其上端接一电源和一固定电阻，电源的电动势E=1.5V,其内阻及导轨的电阻可忽略不计. 固定电阻R=4.5Ω.导体棒ab与导轨垂直且水平，其质量m=3×10-2kg,电阻不计. 整个装置处于竖直向上的匀强磁场中，磁感应强度B=0.5T.(g=10m/s2  sin53º=0.8  cos53º=0.6 )

       （1）将ab棒由静止释放，最终达到一个稳定的速度，求此时电路中的电流；

       （2）求ab稳定时的速度；

       （3）求ab棒以稳定速度运动时电路中产生的焦耳热功率PQ及ab棒重力的功率PG .

            从计算结果看两者大小关系是怎样的？请解释为什么有这样的关系？

    查看答案和解析>>

    如图所示，两条平行的足够长的光滑金属导轨与水平面成α=53°角，导轨间距离L=0.8m．其上端接一电源和一固定电阻，电源的电动势E=1.5V，其内阻及导轨的电阻可忽略不计．固定电阻R=4.5Ω．导体棒ab与导轨垂直且水平，其质量m=3×10-2kg，电阻不计．整个装置处于竖直向上的匀强磁场中，磁感应强度B=0.5T．（g=10m/s2  sin53°=0.8  cos53°=0.6 ）
    （1）将ab棒由静止释放，最终达到一个稳定的速度，求此时电路中的电流．
    （2）求ab稳定时的速度．
    （3）求ab棒以稳定速度运动时电路中产生的焦耳热功率PQ及ab棒重力的功率PG．
    从计算结果看两者大小关系是怎样的？请解释为什么有这样的关系？
    精英家教网

    查看答案和解析>>

    一、选择题（本题共10小题，每小题4分，共40分）

    1．A     2．C D   3．BCD    4．A         5．B D  

    6．B     7．D     8．C D     9．A B       10．D 

    二、填空题（本题共4小题，每小题4分，共16分）

    11．0.8   4   L   0.5   12．45   10   13．     14．0.4  0.2

    三、计算题（本题共4小题，共44分）

    15．（10分）解：（1）设绳断后小球以速度v1平抛

            竖直方向上：2R=g t2         （2分）

    水平方向上：4R=v1t           （2分）  

    解得v1＝2              （1分）

    （2）小球从最低点到最高点过程，小球机械能守恒（选地面为零势能面）

                 （2分）   

    合力提供向心力有：F－mg = m     （2分）

    解得F＝9mg                         （1分）

    16．（10分）解：（1）ab棒受沿斜面向上的安培力F＝BIL，稳定时以速度v匀速下滑。

    说明：因题目中正、余弦值给反了，以此算的答案也给分！

     

     

    解得  I=0.60A                                  （1分）

    （2）闭合电路有 E＝I（R＋r）=0.60A ×(4.5+0.5) W = 3.0V    （2分）

    再由ab棒下滑产生感应电动势E＝BLv                （1分）

    解得 v＝10m/s                                     （1分）

    （3）由感应电流方向判定电容C与a端相连的极板带正电荷   （1分）

    电荷量  Q＝CUR＝CIR＝2.7 ×10－5C                    （2分）

    17．（12分）解：

    （1）设带电粒子经U1电场加速后速度为vo

    由动能定理 qU1=mvo2－0                                    （2分）

    粒子在电场中受电场力F＝Eq,  E=                          （1分）

    做类似平抛运动有：  vx=vo      vy=at    a=   t=           （2分）

    tanq=  解得：  tanq = =         q = 30o                     （2分）

    （2）粒子在磁场中做匀速圆周运动，如图由几何关系得

    圆弧的圆心角为＝30o                               （1分）

    故运动时间t＝，T＝                   （2分）

    解得：B＝      方向垂直纸面向里    （2分）

    18. （12分）解：（1）对铁块有 得  （1分）

    对木板有    得     （2分）

    抽出木板的过程中：

    铁块位移

    木板位移

    两位移之间的关系为   即          （2分）

    解得                           （1分）

    （2）抽出木板的瞬间，铁块的速度大小为       （1分）

    木板的速度大小为                      （1分）

    （3）恒定的拉力做功                                        （1分）

    根据能量转化和守恒定律，系统内能增加   （2分）

    解得                    （1分）

    （也可根据能量转化和守恒定律得 ）

     


    同步练习册答案