
题目列表(包括答案和解析)
(本题满分14分)已知在等边三角形ABC中,点P为线段AB上一点,且![]() .
.
(1)若等边三角形边长为6,且![]() ,求
,求![]() ;
;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
下列命题:①△ABC中,“![]() ”是“△ABC为钝角三角形”的充分但不必要条件;②若
”是“△ABC为钝角三角形”的充分但不必要条件;②若![]() ,且直线
,且直线![]() 为异面直线,则
为异面直线,则![]() ;③△ABC中,
;③△ABC中,![]() 、b、c分别是角A、B、C的对边,已知A=60°,
、b、c分别是角A、B、C的对边,已知A=60°,![]() ,
,![]() ,则S△ABC=6
,则S△ABC=6![]() ;④在条件
;④在条件![]() 不全为0)下,不等式
不全为0)下,不等式![]() 恒成立,则
恒成立,则![]() 的最大值为
的最大值为![]() ,其中正确命题的个数为
,其中正确命题的个数为
A.1 B.2 C.3 D.4
| n(n+1) |
| 2 |
| n(n+1)(n+2) |
| 6 |
| 0+2+6 |
| 4 |
| 2(1+3) |
| 4 |
| 0+3+9+18 |
| 9 |
| 3(1+3+6) |
| 9 |
| 10 |
| 3 |
| an |
| an+1 |
| an+1 |
| an |
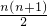 ,前n项和为
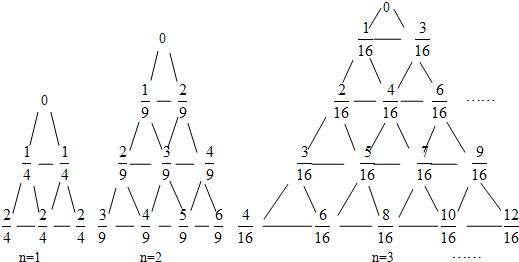
,前n项和为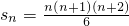 ,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则
,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则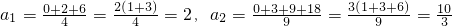 .
.
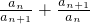 ,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).
,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*). ,前n项和为
,前n项和为 ,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则
,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则 .
.
 ,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).
,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com