题目列表(包括答案和解析)
若直角坐标平面内，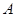
、
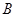两点满足条件： ① 点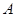、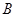都在函数
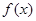图像上；②点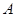、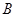关于原点对称，则称点对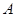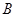（、）是函数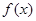的一个“姐妹点对”（点对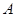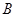（、）与点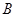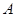（、）可看作同一个“姐妹对”）．
已知函数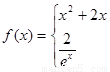
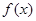，则的“姐妹点对”的个数为
（
）
A．1 B． 2 C． 3 D． 4
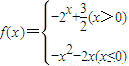，则f（x）的“和谐点对”有（ ）在直角坐标平面内，A点在( 4，0 )，B点在圆 ( x 2 ) 2 + y 2 = 1上，以AB为边作正△ABC （A、B、C按顺时针排列），则顶点C的轨迹是（ ）
（A）圆 （B）椭圆 （C）抛物线 （D）双曲线的一支
若直角坐标平面内，
、
两点满足条件：
① 点、都在函数
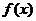图像上；
②点、关于原点对称，则称点对（、）是函数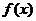的一个“姐妹点对”（点对（、）与点（、）可看作同一个“姐妹对”）．
已知函数
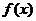，则的“姐妹点对”的个数为 （
）
A．1 B．2 C．3 D．4
在直角坐标平面中,已知点
, 
，…
, 其中n是正整数. 对平面上任一点
, 记A1为A0关于点P1的对称点, A2为A1关于点P2的对称点, ┄, AN为AN-1关于点PN的对称点.
（1）求向量
的坐标;
（2）当点A0在曲线C上移动时, 点A2的轨迹是函数
的图象,其中
是以3为周期的周期函数,且当x∈(0,3)时,=lgx.求以曲线C为图象的函数在(1,4)上的解析式;
（3）对任意偶数n,用n表示向量
的坐标.
一、选择题
题号
1
2
3
4
5
6
7
8
答案
D
A
C
B
D
C
C
A
4．【解析】{an}为等差数列，则{
}也为等差数列且其公差d = 1,
∴
，∴
=
．
5．【解析】圆方程可化为
，则圆心到直线的距离
，当1＜d＜3时，则圆上恰有两个点到直线的距离等于1，
＜|c|＜
，故选D.
6．【解析】y
= f(x)是奇函数，由f(x)＞f (?x) + x得f(x)＞
，数形结合．
7．【解析】设l过原点，取线段AB的中点M(?1，
)，则OM⊥l，∴kl =
．
8．【解析】∵f(x)是偶函数且f(x)在[0，+∞)是增函数
∴|ax + 1|≤|x ?2|恒成立，x∈[
，1]．
∴x ? 2≤ax + 1≤2 ? x
即
．
二、填空题
9．【解析】
，令
有r = 2，∴
．
10．【解析】
= 1440．
11． 【解析】求出交点
代入求出k并验证得k = ?9．
12．
【解析】易求：抛物线焦点F(4，0)，准线L：x = ? 4．椭圆焦点F(4，0)、 F′(4，4)，如图所示．
所以F为两曲线之公共焦点．
设两曲线交于点A，则
所以当H、A、F′共线时，2a有最小值，从而a也达到最小，此时，yA = yF = 4，代入y2 = 16x 得xA = 1，再以A(1，4)代入椭圆得：a2 = 16，从而a = 4．
13．【解析】①在平面A′FA内过点A′作A′H⊥AF，垂足为H，由DE⊥AF，DE⊥A′G知DE⊥平面A′GA．故DE⊥A′H，∴A′H⊥平面ABC，即A′在平面ABC上的射影在线段AF上．
②由①得；
③由①知：当A′H与A′G重合时，三棱锥A′―FED的体积有最大值；
④用反证法：假设A′E与BD垂直，由①知A′H⊥BD，∴BD⊥面A′HE，EH⊥BD．
∴当EH⊥BD时，可证A′E⊥BD．
故①②③正确．
14．【解析】当n≤x＜n + 1(n∈Z)时，y = f(x) = x ? n，
显然有0≤x ? n＜1，即0≤y＜1，
也有f(x+ 1) }= x + 1 ? [x + 1] = x + 1? ([x] + 1) = x ? [x] = f(x)．如图．
答案为：［0，1）；1
15．【解析】（i）20；
（ii）将粒子的运动轨迹定义为数对（i，j）
则它的运动整点可排成数表
（0，0）
（0，1） （1，1） （1，0）
（0，0） （2，1） （2，2） （1，2） （0，2）
（0，3） （1，3） （2，3） （3，3） （3，2） （3，1） （3，0）
（4，0） （4，1） （4，2） （4，3） （4，4） （3，4） （2，4） （1，4）（0，4）
通过推并可知：经过2 = 1×2s，运动到（1，1）
经过6 =2×3s，运动到（2，2）
经过12 =3×4s，运动到（3，3）
∴经过44×45 = 1980s，运动到（44，44）
再继续运动29s，到达点（15，44）．
三、解答题
16．【解析】（1）
= 0，1，2，4．
（1分）
P(= 4) =
P(= 2) =
P(= 1) =
P(= 0) = 1?P(= 1) ?P(= 2) ?P(= 4) =
（7分）
∴的分布列为
0
1
2
4
P
（9分）
∴E=
，
D= (0 ? 1)2×+ (1 ? 1)2×+(2 ? 1)2×+(4 ? 1)2×= 1
（12分）
17．【解析】（Ⅰ）∵
，∴
= 0，
（2分）
∴
，
（4分）
又∵
∈R，∴
时，mmin = ?2.
又
，所以
（6分）
（Ⅱ）∵
，且
,∴
（8分）
∴
∴
（10分）
（12分）
18．【解析】（Ⅰ）∵AB = 3，BC = 4，∴AC = 5
∵AC2 = AB2 + BC2
∴AB⊥BC
又AB⊥BB1
且BC∩BB1 = B
∴AB⊥面BCC1B1 （4分）
（Ⅱ）如图，建立空间直角坐标系
则A(3，0，0)，P(0，0，3)，Q(0，4，4)
设面APQ的法向量为
= (x，y，z)
= (1，?1，1)
而面ABC的法向量可以取
= (0，0，1)
∴
∴面PQA与面ABC所成的锐二面角为arccos
．
（8分）
（Ⅲ）∵BP = AB = 3，CQ = AC = 7．
∴S四边形BCQP
=
∴VA―BCQP
=×20×3 = 20
又∵V
=
．
∴
．
（12分）
19．【解析】（Ⅰ）
（
）． （2分）
（Ⅱ）设第n区内的面积为bn平方米，
则 
． （4分）
则第n区内火山灰的总重量为
（吨）
（万吨） （6分）
设第n区火山灰总重量最大，则
解得
∴n =50.
即得第50区火山灰的总重量最大. （9分）
（Ⅲ）设火山喷发的火山区灰总重量为S万吨，
则
设
则
①
∴
②
①－②得
∴
（12分）
∵0＜q＜1，∴
（万吨）
因此该火山这次喷发出的火山灰的总重量约为3712万吨． （13分）
20．【解析】（Ⅰ）因为圆O的方程为x2 + y2
= 2，所以d
=
，
可得b2 = 2(k2 + 1)(k≠±1)． （4分）
（Ⅱ）设A(x1，y1)，B(x2，y2)，
由
，
所以
，
（7分）
所以
=
=
，
因为|AB| =
×
=
，
O到AB的距离
，
（11分）
所以
=
∈
．
（13分）
21．（Ⅰ）【解析】
．
（2分）
由f (?2) =
又∵b，c∈N* ∴c = 2，b = 2
∴f (x) =
．
（4分）
令f′(x)＞0得：x＜0或x＞2
令f′(x)＜0得：0＜x＜2
∴f(x)的单调递增区间为（?∞，0），（2，+∞）
f(x)的单调递减区间为（0，1），（1，2）． （6分）
（Ⅱ）证明：由已知可得：2Sn = an ? 
，
两式相减得：(an + an ? 1) (an ? an ? 1+1) = 0 （n≥2）
∴an = ?an ?1或an ?an?1 = ?1 （7分）
当n =1 时，2a1 = a1 ?
若an = ?an?1，则a2 = ?a1 = 1与an≠1矛盾．
（定义域要求an≠1）
∴an ? an?1 = 1，∴an = ?n． （8分）
要证的不等式转化为
先证不等式
令g (x) = x ?ln(1 + x)，h(x) = ln(x +1) ?
（10分）
则g′(x) =
，h′(x) =
∵x＞0 ∴g′(x)＞0，h′(x)＞0
∴g (x)， h(x)在（0，+∞）上
∴g (x)＞g (0) = 0，h(x)＞h(0) = 0 （12分）
∴
故
，即
．
（13分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com