
题目列表(包括答案和解析)
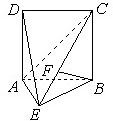 如图,DA⊥平面ABE,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,DA⊥平面ABE,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.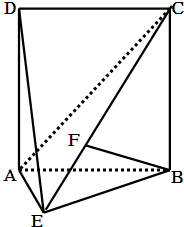 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE. 如图,直二面角D-AB-E中,四边形ABCD是正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.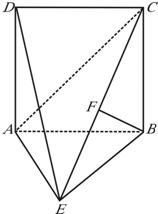 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
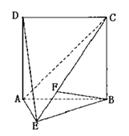
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F
为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的余弦值;
(Ⅲ)求点D到平面ACE的距离.
一、选择题(每题5分,共60分)
1―5 ACCBA 6―10 BCABD 11―12 DB
|