
题目列表(包括答案和解析)
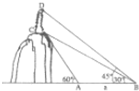 (2011•开封一模)如图,山顶上有一塔,为了测量塔高,测量人员在山脚下A点处测得塔底C的仰角为60°,移动am后到达B点,又测得塔底C点的仰角为30°,测得塔尖D点的仰角为45°,求塔高CD.
(2011•开封一模)如图,山顶上有一塔,为了测量塔高,测量人员在山脚下A点处测得塔底C的仰角为60°,移动am后到达B点,又测得塔底C点的仰角为30°,测得塔尖D点的仰角为45°,求塔高CD.
如图,在山顶上有一塔,为了测量塔高,测量人员在山脚下A点处测得塔底C的仰角为600,移动100m后到达B点,又测得塔底C点得仰角为300,测得塔尖D的仰角为450,求塔高CD.
【解析】本试题主要是考查了解三角形中正弦定理的运用以及余弦定理的综合运用。
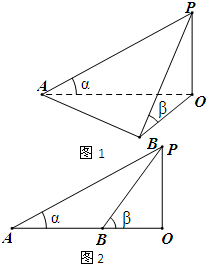 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.| 4 | d |
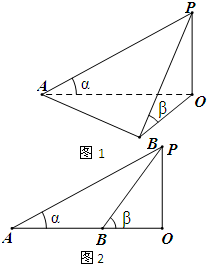 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.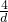 ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大?一、选择题:本小题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
B
C
A
C
B
B
A
A
二、填空题:本小题11―13题必答, 14、15小题中选答1题,若全答只计14题得分,共20分.
11. 35 12.  13.
13. 
14.
 或
或 15.
15. 

三、解答题:共80分.
16题(本题满分13分)
解:(1)要使f(x)有意义,必须 ,即
,即
得f(x)的定义域为 ………………………………7分
………………………………7分
(2)因f(x)的定义域为 ,关于原点不对称,所以
,关于原点不对称,所以
f(x)为非奇非偶函数. ……………………………………………13分
17题(本题满分13分)
解:(1)当且仅当 时,方程组有唯一解.因
时,方程组有唯一解.因 的可能情况为
的可能情况为 三种情况………………………………3分
三种情况………………………………3分
而先后两次投掷骰子的总事件数是36种,所以方程组有唯一解的概率
 ……………………………………………………………………6分
……………………………………………………………………6分
(2)因为方程组只有正数解,所以两直线的交点在第一象限,由它们的图像可知
 ………………………………………………………………9分
………………………………………………………………9分
解得(a,b)可以是(1,4),(1,5),(1,6),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2),(5,1),(5,2),(6,1),(6,2),所以方程组只有正数解的概率 ………………………………………………………………………13分
………………………………………………………………………13分
18题(本题满分14分)
(1) 证明:由题设知,FG=GA,FH=HD
所以GH
 .
.
又BC
 ,故GH
,故GH BC
BC
所以四边形BCHG是平等四边形。……………………4分
(2) C、D、F、E四点共面。理由如下:
由BE
 ,G是FA的中点知,
,G是FA的中点知,
BE GF,所以EF//BG。……………………6分
GF,所以EF//BG。……………………6分
由(1)知BG//CH,故EF//CH,故F、E、C、H共面,又点D在直线FH上,
所以C、D、F、E四点共面。……………………8分
(3)
证明:连结EG,由AB=BE,BE AG,及
AG,及 ,知ABEG是正方形,
,知ABEG是正方形,
故BG⊥EA。由题设知,FA、AD、AB两两垂直,故AD⊥平面FABE,因此AD⊥BG,又EA∩AD=A,所以BG⊥平面ADE。
由(1)知,CH//BG,所以CH⊥平面ADE,由(2)知H 平面CDE,故CH
平面CDE,故CH 平面CDE,得平面ADE⊥平面CDE。……………………14分
平面CDE,得平面ADE⊥平面CDE。……………………14分
19题(本题满分14分)
解:(1)由已知得 ,解得:
,解得: ……………………4分
……………………4分
所求椭圆方程为 ………………………………………………6分
………………………………………………6分
(2)因点 即A(3,0),设直线PQ方程为
即A(3,0),设直线PQ方程为 ………………8分
………………8分
则由方程组 ,消去y得:
,消去y得:
设点 则
则 ……………………11分
……………………11分
因 ,得
,得 ,
,
又 ,代入上式得
,代入上式得
 ,故
,故
解得: ,所求直线PQ方程为
,所求直线PQ方程为 ……………………14分
……………………14分
20题(本题满分14分)
解:(1)函数f(x)的定义域为 ,
, …………2分
…………2分
①当 时,
时, >0,f(x)在
>0,f(x)在 上递增.………………………………4分
上递增.………………………………4分
②当 时,令
时,令 得
得 解得:
解得:
 ,因
,因 (舍去),故在
(舍去),故在 上
上 <0,f(x)递减;在
<0,f(x)递减;在 上,
上, >0,f(x)递增.……………8分
>0,f(x)递增.……………8分
(2)由(1)知 在
在 内递减,在
内递减,在 内递增.
内递增.
 ……………………………………11分
……………………………………11分
故 ,又因
,又因
故 ,得
,得 ………………14分
………………14分
21题(本题满分12分)
解:(1)由 ,可得
,可得
 ………………………………3分
………………………………3分
所以 是首项为0,公差为1的等差数列.
是首项为0,公差为1的等差数列.
所以 即
即 ……………………6分
……………………6分
(2)解:设 ……①
……①
 ……②
……②
当 时,①
时,① ②得
②得

 …………9分
…………9分
这时数列 的前n项和
的前n项和
当 时,
时, ,这时数列
,这时数列 的前n项和
的前n项和
 …………………………………………12分
…………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com