
题目列表(包括答案和解析)
已知函数f(x)=x3-2x2+ax+1(a∈R),若函数f(x)在区间(,1)内是减函数,则a的取值范围是 .
| 1 |
| x-2 |
| 1 |
| 2 |
(本题满分12分)
设函数f(x)=x3+ax2-3x+b(a,b∈R)在x=x1,x=x2处取得极值,且|x1-x2|=2(1)求a的值及函数f(x)的单调区间; (2)若存在x0∈(x1,x2),使得f(x0)=0,求b的取值范围
(12分)
设函数f(x)= x3-3ax+b (a≠0).
(Ⅰ)若曲线y= f(x)在点(2,f(x))处与直线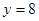 相切,求
相切,求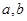 的值;
的值;
(Ⅱ)求函数f(x)的单调区间与极值点.
(1)a的值;
(2)函数f(x)的单调区间.
高三数学试卷(文科) 2009.1
一、选择题:本大题共8小题,每小题5分,共40分.
题号
1
2
3
4
5
6
7
8
答案
D
B
A
B
C
C
B
C
二、填空题:本大题共6小题,每小题5分,共30分.
9.x2-.files/image033.gif) =1 10.14 11.160 12.16π,
=1 10.14 11.160 12.16π, .files/image035.gif) π 13.①② 14.-3x2+6
π 13.①② 14.-3x2+6
注:两空的题目,第一个空2分,第二个空3分.
三、解答题:本大题共6小题,共80分.
15.(本小题满分12分)
(Ⅰ)解:因为cos B=2cos2.files/image024.gif) -1=
-1=.files/image038.gif) ,
…………………………3分
,
…………………………3分
在△ABC中,由余弦定理b2= a2+c2-2accos B,
得b2=16+9-24×.files/image038.gif) =22,
=22,
所以b=.files/image040.gif) ;
…………………………6分
;
…………………………6分
(Ⅱ)解:由(Ⅰ)知cos B=.files/image038.gif) ,B∈(0, π),
,B∈(0, π),
所以sim B=.files/image042.gif) ,
…………………………9分
,
…………………………9分
由三角形的面积公式S=.files/image044.gif) acsin B,
acsin B,
得S=.files/image044.gif) ×4×3×
×4×3×.files/image046.gif) =
=.files/image048.gif) .
.
所以△ABC的面积为.files/image048.gif) .
…………………………12分
.
…………………………12分
16.(本小题满分12分)
(Ⅰ)解:记“至少有2件甲批次产品检验不合格”为事件A. ……………1分
由题意,事件A包括以下两个互斥事件:
①事件B:有2件甲批次产品检验不合格.由n次独立重复试验中某事件发生k次的概率公式,得P(B)=C23.files/image050.gif) ; ……………… 3分
; ……………… 3分
高三数学(文科)答案 第1页(共8页)
②事件C:3件甲批次产品检验都不合格.由相互独立事件概率乘法公式,得
P(C)=(.files/image027.gif) )3=
)3=.files/image053.gif) ;
;
所以,“至少有2件甲批次产品检验不合格”的概率为P(A)= P(B)+ P(C)= .files/image055.gif) ;
;
……………… 6分
(Ⅱ)解:记“甲批次产品检验不合格件数比乙批次产品检验不合格件数多2件”为事件D.由题意,事件D包括以下两个互斥事件:
① 事件E:3件甲批次产品检验都不合格,且有1件乙批次产品检验不合格.其概率
P(E)=(.files/image027.gif) )
).files/image057.gif) C13(
C13(.files/image029.gif) )1(1-
)1(1-.files/image029.gif) )2=
)2=.files/image060.gif) ;
……………… 9分
;
……………… 9分
② 事件F:有2件甲批次产品检验不合格,且有0件乙批次产品检验不合格.其概率
P(F)=C23(.files/image027.gif) )2(1-
)2(1-.files/image027.gif) ).(1-
).(1-.files/image029.gif) )3=
)3=.files/image062.gif) ;
;
所以,事件D的概率为P(D)= P(E)+ P(F)= .files/image064.gif) …………… 12分
…………… 12分
17.(本小题满分14分)
方法一:(Ⅰ)证明:∵平面PCD⊥平面ABCD.
.files/image066.jpg) 又平面PCD∩平面ABCD=CD,BC⊥CD.
又平面PCD∩平面ABCD=CD,BC⊥CD.
∴BC⊥平面PCD, ……………………3分
∵PD.files/image068.gif) 平面PCD,
平面PCD,
∴BC⊥PD; …………………4分
(Ⅱ)解:取PD的中点E,连接CE、BE,
∵△PCD为正三角形,
∴CE⊥PD,
由(Ⅰ)知BC⊥平面PCD,
∴CE是BE在平面PCD内的射影.
∴BE⊥PD,
∴∠CEB为二面角B-PD-C的平面角, ……………………7分
在△CEB中,∠BCE=90°,BC=2,CE=.files/image070.gif) ,
,
∴tan∠CEB=.files/image072.gif) =
=.files/image074.gif) ,
,
∴二面角B-PD-C的大小为arctan.files/image074.gif) ;
…………………10分
;
…………………10分
高三数学(文科)答案 第2页(共8页)
(Ⅲ)解:过D作DF⊥PC于F,
∵BC⊥平面PCD,
∴BC⊥DF.
∵PC∩BC=C.
∴DF⊥平面PBC,且BF∩平面PBC=F,
∴DF为点D到平面PBC的距离, …………………13分
在等边△PCD中, DC=2, DF⊥PC,
∴CF=1,DF=.files/image076.gif) ,
,
∴点A到平面PBC的距离等于.files/image070.gif) .
…………………14分
.
…………………14分
方法二:(Ⅰ)证明:取CD的中点为O,连接PO,
.files/image079.jpg) ∵PD=PC,∴PO⊥CD,
∵PD=PC,∴PO⊥CD,
∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,
∴PO⊥平面ABCD, ………………………2分
如图,在平面ABCD内,过O作OM⊥CD交AB于M,
以O为原点,OM、OC、OP分别为x、y、z轴,建立空间
直角坐标系O-xyz,
则B(2,1,0),C(0,1,0),D(0,-l,0),P(0,0,.files/image070.gif) ),
),
∵.files/image082.gif) =(0,-l,-
=(0,-l,-.files/image070.gif) ),
),.files/image084.gif) =(-2,0,0),
=(-2,0,0),
∴.files/image082.gif) ?
?.files/image084.gif) =0,
=0,
∴BC⊥PD; …………………4分
(Ⅱ)解:取PD的中点E,连接CE、BE,如(Ⅰ)建立空间坐标系,则E(0,-.files/image044.gif) ,
,.files/image087.gif) ),
),
∵△PCD为正三角形,
∴CE⊥PD,
∵.files/image089.gif) =(-2,-2,0),
=(-2,-2,0),.files/image091.gif) =(-2,-1,
=(-2,-1,.files/image070.gif) ),
),
∴.files/image093.gif) =
=.files/image095.gif) =
=.files/image097.gif) ,
,
∴BE⊥PD,
∴∠CEB为二面角B-PD- C的平面角, ………………………7分
高三数学(文科)答案 第3页(共8页)
∵.files/image099.gif) =(2,
=(2,.files/image101.gif) ,-
,-.files/image087.gif) ),
),.files/image104.gif) =(0,
=(0,.files/image101.gif) ,-
,-.files/image087.gif) ),
),
∴cos∠BEC=.files/image106.gif) =
=.files/image108.gif) =
=.files/image110.gif) ,
,
∴二面角B-PD- C的大小为arccos.files/image110.gif) ……………10分
……………10分
(III)解:过点D作DF⊥平面PBC于F,
∴DF为点D到平面PBC的距离,设.files/image112.gif) =h,
=h,
∵.files/image084.gif) =(-2,0,0),
=(-2,0,0),.files/image115.gif) = (0,-1,
= (0,-1,.files/image070.gif) ),
),
∴.files/image118.gif) =0,即BC⊥CP,
=0,即BC⊥CP,
∴△PBC的面积S△PBC=.files/image044.gif) |BC|?|PC|=2,
|BC|?|PC|=2,
∵三棱锥D-PBC的体积VD-PBC=VP-BCD,
∴.files/image121.gif) S△PBC
S△PBC.files/image123.gif) =
=.files/image121.gif) S△BCD
S△BCD.files/image125.gif) ,即
,即.files/image127.gif) ,解得h=
,解得h=.files/image070.gif) ,
,
∴点D到平面PBC的距离为.files/image070.gif) .
……………14分
.
……………14分
18.(本小题满分14分)
(Ⅰ)解:函数f(x)的导数 f′(x)= x2-4x+a, ………………2分
由题意,得f′(2)=-4+a=-1,
所以a=3,
故f(x)=.files/image029.gif) x3-2 x2+3 x;
………………5分
x3-2 x2+3 x;
………………5分
(Ⅱ)解:由(Ⅰ)知f′(x)= x2-4 x+3,
由f′(x)= x2-4 x+3=0,得x=1,或x=3.
x变化时,f′(x),f(x)的变化情况如下表:
x
(-∞,1)
1
(1,3)
3
(3,+∞)
f′(x)
+
0
-
0
+
f(x)
.files/image130.gif)
极大值.files/image132.gif)
.files/image134.gif)
极小值0
.files/image130.gif)
………………8分
高三数学(文科)答案 第4页(共8页)
所以,当b.files/image136.gif) 1或b-1
1或b-1.files/image138.gif) 3时,函数f(x)无极值; ……………………10分
3时,函数f(x)无极值; ……………………10分
当b-1<1,且b>1时,函数f(x)在x=1时,有极大值.files/image132.gif) ,此时函数无极小值;
,此时函数无极小值;
当b-1<3,且b>3时,函数f(x)在x=3时,有极小值0,此时函数无极大值;
当b-1.files/image138.gif) 1,且b
1,且b.files/image136.gif) 3时, 函数f(x)无极值. ……………………13分
3时, 函数f(x)无极值. ……………………13分
故当b∈(-∞,1]∪[2,3]∪[4,+ ∞)时,函数f(x)无极值;
当b∈(1,2)时,函数f(x)在x=1时,有极大值.files/image132.gif) ,此时函数无极小值;
,此时函数无极小值;
当b∈(3,4)时,函数f(x)在x=3时,有极小值0,此时函数无极大值.………14分
19.(本小题满分14分)
方法一:(Ⅰ)解:由题意,得F(1,0),直线l的方程为y=x-1.
由.files/image140.gif) ,得x2-6 x +1=0,
,得x2-6 x +1=0,
设A,B两点坐标为A (x1,y1),B(x2,y2),AB中点M的坐标为M(x0,y0),
则x1=3+2.files/image020.gif) ,x2=3-2
,x2=3-2.files/image020.gif) ,y1= x1-1=2+2
,y1= x1-1=2+2.files/image020.gif) ,y2= x2-1=2―2
,y2= x2-1=2―2.files/image020.gif) ,
,
故点A(3+2.files/image020.gif) ,2+2
,2+2.files/image020.gif) ),B(3-2
),B(3-2.files/image020.gif) ,2-2
,2-2.files/image020.gif) ),
……………3分
),
……………3分
所以x0=.files/image143.gif) =3,y0= x0-1=2,
=3,y0= x0-1=2,
故圆心为M(3,2),直径.files/image145.gif) =
=.files/image147.gif) ,
,
所以以AB为直径的圆的方程为(x-3)2+( y-2)2=16; ………………6分
(Ⅱ)解:因为.files/image149.gif) =2
=2.files/image151.gif) ,三点A,F,B共线且点A,B在点F两侧,
,三点A,F,B共线且点A,B在点F两侧,
所以.files/image153.gif) =
=.files/image155.gif) ,
,
设A,B两点坐标为A (x1,y1),B(x2,y2),则.files/image153.gif) =(x1-1,y1),
=(x1-1,y1),.files/image157.gif) (1-x2,-y2),
(1-x2,-y2),
所以.files/image159.gif) ①
①
因为点A,B在抛物线C上,
所以y12=4x1,y22=4x2, ② ………………10分
高三数学(文科)答案 第5页(共8页)
由①②,解得.files/image161.gif) 或
或.files/image163.gif)
所以A(2,2.files/image020.gif) ),B(
),B(.files/image044.gif) ,-
,-.files/image020.gif) ),或A(2,-2
),或A(2,-2.files/image020.gif) ),B(
),B(.files/image044.gif) ,
,.files/image020.gif) ),………13分
),………13分
故直线l的方程为2.files/image020.gif) x-y-2
x-y-2.files/image020.gif) =0,或2
=0,或2.files/image020.gif) x+y-2
x+y-2.files/image020.gif) =0. ………14分
=0. ………14分
方法二:(Ⅰ)解:由题意,得F(1,0),直线l的方程为y=x-1.
由.files/image140.gif) ,得x2-6x+1=0,
,得x2-6x+1=0,
设A, B两点坐标为A(x1,y1),B(x2,y2),AB中点M的坐标为M(x0,y0),
因为△=62-4=32>0,所以x1+ x2=6, x1x2=1,
所以x0=.files/image143.gif) =3,y0= x0-1=2,故圆心为M(3,2),
………………3分
=3,y0= x0-1=2,故圆心为M(3,2),
………………3分
由抛物线定义,得.files/image145.gif) =
=.files/image170.gif) +
+.files/image151.gif) =(x1+
=(x1+.files/image173.gif) )+(x2+
)+(x2+.files/image173.gif) )= x1+ x2+p=8,
)= x1+ x2+p=8,
所以.files/image145.gif) = x1+ x2+P=8(其中p=2).
= x1+ x2+P=8(其中p=2).
所以以AB为直径的圆的方程为(x-3)2+( y-2)2=16; ………………6分
(Ⅱ)解:因为.files/image149.gif) =2
=2.files/image151.gif) ,三点A, F,B共线且点A, B在点F两侧,
,三点A, F,B共线且点A, B在点F两侧,
所以.files/image153.gif) =2
=2.files/image157.gif) ,
,
设A, B两点坐标为A(x1,y1),B(x2,y2)则.files/image153.gif) =(x1-1,y1),
=(x1-1,y1),.files/image157.gif) =(1-x2,-y2),
=(1-x2,-y2),
所以.files/image159.gif) ①
………………9分
①
………………9分
设直线AB的方程为y= k(x-1)或x=1(不符合题意,舍去).
由.files/image179.gif) ,消去x得ky2-4y-4k=0,
,消去x得ky2-4y-4k=0,
因为直线l与C相交于A, B两点,所以k≠0,
则Δ=16+16k2>0,y1+y2=.files/image181.gif) ,y1 y2=-4,
②
,y1 y2=-4,
②
高三数学(文科)答案 第6页(共8页)
由①②,得方程组.files/image183.gif) ,解得
,解得.files/image185.gif) 或
或.files/image187.gif) ,……13分
,……13分
故直线l的方程为.files/image097.gif) x- y-
x- y-.files/image097.gif) =0,或
=0,或.files/image097.gif) x + y-
x + y-.files/image097.gif) =0. ……14分
=0. ……14分
20.(本小题满分14分)
(Ⅰ)解:∵数列{an+Sn}是公差为2的等差数列,
∴(an+1+Sn+1)-(an+Sn)=2,
即an+1=.files/image190.gif) ,
……2分
,
……2分
∵a1=1,
∴a2=.files/image101.gif) ,a3=
,a3=.files/image193.gif) ;
……4分
;
……4分
(Ⅱ)证明:由题意,得a1-2=-1,
∵.files/image195.gif)
∴{an-2}是首项为-1,公比为.files/image044.gif) 的等比数列;
……8分
的等比数列;
……8分
(Ⅲ)解:由(Ⅱ)得an-2=-(.files/image044.gif) )n-1,
)n-1,
∴an
=2-(.files/image044.gif) )n-1,
)n-1,
∵{an+Sn}是首项为a1+ S1=2,公差为2的等差数列,
∴an+Sn=2+(n-1)×2=2n,
∴Sn=2n-2+(.files/image044.gif) )n-1,
……9分
)n-1,
……9分
设存在整数λ,使不等式Sn-n+ 1.files/image138.gif) λan对任意的n∈N*成立,
λan对任意的n∈N*成立,
即存在整数λ,使不等式n-1+(.files/image044.gif) )n-1
)n-1.files/image138.gif) λ[2-(
λ[2-(.files/image044.gif) )n-1]对任意的n∈N*成立,
)n-1]对任意的n∈N*成立,
∴当n=1时,不等式成立,解得λ.files/image136.gif) 1,
……10分
1,
……10分
以下证明存在最大的整数λ=1,使不等式Sn-n+ 1.files/image138.gif) λan对任意的n∈N*成立.
λan对任意的n∈N*成立.
高三数学(文科)答案 第7页(共8页)
当n=2时,不等式化简为.files/image200.gif) ,成立;
,成立;
当n.files/image138.gif) 3时,∵(Sn-n+ 1)-an=n-3+(
3时,∵(Sn-n+ 1)-an=n-3+(.files/image044.gif) )n-2>0,
)n-2>0,
∴(Sn-n+ 1)>an成立.
综上,知存在整数λ,使不等式Sn-n+ 1.files/image138.gif) λan对任意的n∈N*成立,且λ的最大值为1.
λan对任意的n∈N*成立,且λ的最大值为1.
……14分
高三数学(文科)答案 第8页(共8页)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com