练习册

  • 练习册
  • 试题
    (II)若在上的最小值为.求在R上的极大值. 【查看更多】

     

    题目列表(包括答案和解析)

    已知定义在R上的二次函数R（x）=ax2+bx+c满足2R（-x）-2R（x）=0，且R（x）的最小值为0，函数h（x）=lnx，又函数f（x）=h（x）-R（x）．
    （I）求f（x）的单调区间；  
    （II）当a≤
    1
    2
    时，若x0∈[1，3]，求f（x0）的最小值；
    （III）若二次函数R（x）图象过（4，2）点，对于给定的函数f（x）图象上的点A（x1，y1），当x1=
    3
    2
    时，探求函数f（x）图象上是否存在点B（x2，y2）（x2＞2），使A、B连线平行于x轴，并说明理由．（参考数据：e=2.71828…）

    查看答案和解析>>

    .已知定义在R上的二次函数满足，且的最小值

    为0，函数，又函数。

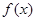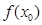    （I）求的单调区间；  （II）当≤时，若，求的最小值；

    （III）若二次函数图象过（4，2）点，对于给定的函数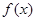图象上的点A（），

    当时，探求函数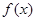图象上是否存在点（）（），使、连线平行于轴，并说明理由。（参考数据：e=2.71828…）

     

     

     

    查看答案和解析>>

    已知定义在R上的二次函数满足，且的最小值为0，函数，又函数。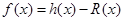

    （I）求的单调区间；

    （II）当≤时，若，求的最小值；

    （III）若二次函数图象过（4，2）点，对于给定的函数图象上的点A（），当时，探求函数图象上是否存在点B（）（），使A、B连线平行于x轴，并说明理由。

    （参考数据：e=2.71828…）

     

    查看答案和解析>>

    已知定义在R上的二次函数R（x）=ax2+bx+c满足2R（-x）-2R（x）=0，且R（x）的最小值为0，函数h（x）=lnx，又函数f（x）=h（x）-R（x）．
    （I）求f（x）的单调区间；  
    （II）当a≤
    1
    2
    时，若x0∈[1，3]，求f（x0）的最小值；
    （III）若二次函数R（x）图象过（4，2）点，对于给定的函数f（x）图象上的点A（x1，y1），当x1=
    3
    2
    时，探求函数f（x）图象上是否存在点B（x2，y2）（x2＞2），使A、B连线平行于x轴，并说明理由．（参考数据：e=2.71828…）

    查看答案和解析>>

    已知定义在R上的二次函数R（x）=ax2+bx+c满足2 R（﹣x）﹣2 R（x）=0，且R（x）的最小值为0，函数h（x）=lnx，又函数f（x）=h（x）﹣R（x）．
    （I）求f（x）的单调区间； 
    （II）当a≤时，若x0∈[1，3]，求f（x0）的最小值；
    （III）若二次函数R（x）图象过（4，2）点，对于给定的函数f（x）图象上的点A（x1，y1），当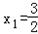时，探求函数f（x）图象上是否存在点B（x2，y2）（x2＞2），使A、B连线平行于x轴，并说明理由．（参考数据：e=2.71828…）

    查看答案和解析>>

    一、选择题：每小题5分，共60分．

           BABDB   DCABD  BD

    二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卷相应题号的横线上．

    13．某校有教师200人，男学生1200人，女学生1000人，现用分层抽样的方法从所有老师中抽取一个容量为n的样本；已知从女学生中抽取的人数为80人，则n的值为：16

    14．若△ABC三个内角A、B、C的对边分别是a、b、c，且acosB+bcosA=csinC，则角C的大小为：

    15．若、满足约束条件的最大值为：2

    16．若，且，则实数x的取值范围是：

    三、解答题：本大题共6小题，共70分．把答案填在答题卷相应题号的答题区中．

    17．（本小题满分10分）

    如图，已知，，且，．

    （I）试用表示；

    （Ⅱ）设向量和的夹角为，求的值．

    解：（I）设，则

          ，；            …………3分

    因，，，

           所以         解得：                                                  

           即 ．                                                                                  …………5分

    （Ⅱ）由（I）知 ，又，

    所以 ) ()=，                                     

                                …………8分

    故 ．                                                      …………10分

    18．（本小题满分10分）

    甲、乙等五名奥运志愿者被随机地分配到四个不同的岗位服务，每个岗位至少有一名志愿者．

    （Ⅰ）求甲、乙两人同时被分配到岗位服务的概率；

    （Ⅱ）求甲、乙两人被分配到不同岗位服务的概率．

    解：（Ⅰ）记甲、乙两人同时被分到岗位服务为事件，

    那么，

    即甲、乙两人同时被分到岗位服务的概率是．                                       …………5分

    （Ⅱ）设甲、乙两人同时被分到同一岗位服务为事件，

    那么，

    故甲、乙两人被分到不同岗位服务的概率是．         …………10分

    19．（本小题满分12分）

    如图，四面体ABCD中，O是BD的中点，AB=AD=，CA=CB=CD=BD=2．

    （Ⅰ）求证：AO⊥平面BCD；

    （Ⅱ）求异面直线AB与CD所成角的大小．

     

    解:(方法一)

    （Ⅰ）连结OC．∵BO=DO，AB=AD， BC=CD，

    ∴AO⊥BD，CO⊥BD．                                        …………3分

    在△AOC中，由已知得AC=2，AO=1，CO=，

    ∴AO2+CO2=AC2，∴∠AOC=90°，即AO⊥OC．

     ∴AO平面BCD．            …………6分

    （Ⅱ）分别取AC、BC的中点M、E，连结OM、ME、OE，则

                      ME∥AB，OE∥DC．     

    ∴（或其补角）等于异面直线AB与CD所成的角．                    …………9分

    在△OME中，                                   

    又 是直角△AOC斜边AC上的中线，∴

    ∴

    ∴异面直线AB与CD所成角的大小为                                                 …………12分

    (方法二)

    （Ⅰ）同方法一．                                                …………6分

    （Ⅱ）由（Ⅰ）知：AO⊥OC，AO⊥BD，CO⊥BD．

    以O为原点，建立空间直角坐标系如图，   …………7分

    则A(0，0，1)，B(1，0，0)，C(0，，0)，D(-1，0，0) ．        …………10分

    所以 ，

    ∴异面直线AB与CD所成角的大小为                                         …………12分

    20．（本小题满分12分）

    数列满足，且．

       （I）求，并证明数列是等比数列；

       （II）求．

    解：（I），

               ；                       …………2分

      又，，                    …………4分

        且  

        所以数列是以-2为首项，3为公比的等比数列．                   …………6分

       （II）由（I）得，    ．                  …………8分

       

                                   …………10分

                                        …………12分

    21.（本小题满分13分）

    已知函数，在任意一点处的切线的斜率为.

    （I）求函数的单调区间；

    （II）若在上的最小值为，求在R上的极大值.

    21. 解：（I）因,所以；  …………2分

    故  , ，，，

     ,   .                  …………4分

    由知在和上是增函数，

    由知在（-1，2）上为减函数.               …………8分

    （II）由（I）知在（-3，-1）上是增函数，在（-1，2）上为减函数，

    所以 在上的最小值是或，极大值为.       …………10分

    而，,，

    ∴在上的最小值是,∴,.   …………12分

    ，

    即所求函数在R上的极大值为                                 …………13分

    22．（本小题满分13分）

    如图，倾斜角为的直线经过抛物线的焦点F，且与抛物线交于A、B两点．

    （I）求抛物线的焦点F的坐标及准线l的方程；

    （II）若为锐角，作线段AB的垂直平分线m交x轴于点P，证明为定值，并求此定值．

    解：（I）设抛物线的标准方程为，则，从而．

    因此抛物线焦点F的坐标为（2，0），准线方程为．                      ……………4分

    （II）作AC⊥l，BD⊥l，垂足分别为C、D，

    则由抛物线的定义知：|FA|=|AC|，|FB|=|BD|．

    记A、B的横坐标分别为xA、xB，则

    |FA|＝|AC|＝

    解得；                                          ……………7分

    |FB|＝|BD|＝

    解得．                                                                           ……………9分

    记直线m与AB的交点为E，则

    ，

    所以．                                                                  ……………12分

    故．                 ……………13分

     

     

     

     


    同步练习册答案