
题目列表(包括答案和解析)
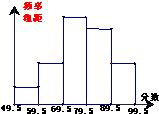 6、某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有( )人.
6、某校对初三学生进行了一次数学应用问题小测验,如图是将(1)班60名同学的成绩进行整理后,分成5组画出的频率分布直方图.已知从左到右四个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次测验中成绩优秀(分数大于或等于80分为优秀)的有( )人.| d2 |
| d1 |
| ||
| 2 |
| a2 |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| a2-b2 |
下面给出一个问题的算法:
S1 输入x.
S2 若x≤2,则执行S3;否则执行S4.
S3 输出-2x-1.
S4 输出x2-6x+3.
问题:
(1)这个算法解决的是什么问题?
(2)当输入的x值为多大时,输出的数值最小?
如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:

(1)这个几何体是什么体?
(2)如果面 在几何体的底部,那么哪一个面会在上面?
在几何体的底部,那么哪一个面会在上面?
(3)如果面 在前面,从左面看是面
在前面,从左面看是面 ,那么哪一面会在上面?
,那么哪一面会在上面?
(4)从右边看是面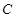 ,面
,面 在后面,那么哪一面会在上面?
在后面,那么哪一面会在上面?
在数学中“所有”一词,叫全称量词,用符号“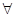 ”表示;“存在”一词,叫做存在量词,用符号“
”表示;“存在”一词,叫做存在量词,用符号“ ”表示。设
”表示。设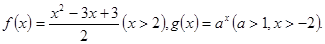 ①若
①若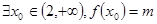 成立,则实数m取值范围为_____________;②若
成立,则实数m取值范围为_____________;②若 则实数a的取值范围为________。
则实数a的取值范围为________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com