
题目列表(包括答案和解析)
| a |
| b |
. |
| a |
| b |
| a |
| b |
| a |
| b |
| BC |
| AB |
| AC |
| AB |
| m |
| n |
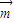 =(2a+c,b)与平面向量
=(2a+c,b)与平面向量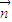 =(cosB,cosC)垂直.
=(cosB,cosC)垂直.集合D={平面向量},定义在D上的映射f,满足对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).
(1)若|a|=|b|,且a与b不共线,试证明:[f(a)-f(b)]⊥(a+b);
(2)若A(1,2),B(3,6),C(4,8),且f![]()
![]()
![]() =
=![]() ,求f(
,求f(![]() )·
)·![]() .
.
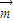 =(2a+c,b)与平面向量
=(2a+c,b)与平面向量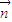 =(cosB,cosC)垂直.
=(cosB,cosC)垂直.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com