
题目列表(包括答案和解析)
直线与圆相交时,求弦长,你有哪些计算方法?常规方法的缺点是计算量较大,但思路清晰;那联立直线方程和圆的方程,你能通过不解方程而利用根与系数的关系及两点间的距离公式来进行计算吗?再想一下,圆又有哪些几何性质?特别是半径、弦心距与半弦长构成的三角形是什么三角形,你能利用它来进行快速地计算吗?
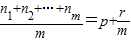 (p∈N*,r∈N且r<m),则
(p∈N*,r∈N且r<m),则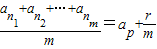 d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.
d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.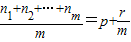 (p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.
(p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.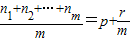 (p∈N*,r∈N且r<m),则
(p∈N*,r∈N且r<m),则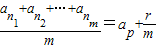 d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.
d;特别地,当r=0时,称ap为an1,an2,…anm的等差平均项.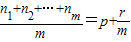 (p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.
(p∈N*,r∈N且r<m),则 ;特别地,当r=0时,称ap为an1,an2,…anm的等比平均项.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com