练习册

  • 练习册
  • 试题
    如图E.F.G.H分别为正方体AC1的棱A1B1.A1D1.B1C1.D1C1的中点.求证(1)E.F.G.H四点共面 (2)平面AEF∥平面BDHG 【查看更多】

     

    题目列表(包括答案和解析)

    正方体是常见并且重要的多面体，对它的研究将有助于我们对立体几何一些概念的理解和掌握．如图所示，在正方体AC1中，E、F、G、H分别是所在棱的中点，请思考并回答下列问题：

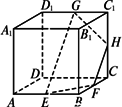
    (1)点E、F、G、H共面吗？

    (2)直线EF、GH、DG能交于一点吗？

    (3)若E、F、G、H四点共面，怎样才能画出过四点E、F、G、H的平面与正方体的截面？

    (4)若正方形的棱长为a，那么(3)中的截面面积是多少？

    查看答案和解析>>

    6、如图，在正方体ABCD-A1B1C1D1中，E、F、G、H分别为AA1、AB、BB1、BC1的中点，则异面直线EF与GH所成的角等于（　　）

    查看答案和解析>>

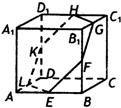    7、如图，在正方体ABCD-A1B1C1D1中，E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点，则六边形EFGHKL在正方体面上的射影可能是（　　）

    查看答案和解析>>

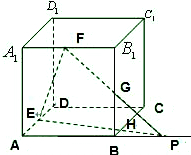    精英家教网如图所示，在正方体ABCD-A1B1C1D1中，其边长为2，E、F分别是AD，A1B1的中点，G、H是BB1，BC的两个动点，
    （1）若直线FG与EH相交于点P，求证：P∈AB
    （2）在（1）的条件下，若G是BB1，的中点，求GH的长．

    查看答案和解析>>

    如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
    （1）求GH长的取值范围；
    （2）当GH取得最小值时，求证：EH与FG共面；并求出此时EH与FG的交点P到直线B1B的距离．

    查看答案和解析>>


    同步练习册答案