练习册

  • 练习册
  • 试题
    解:[方法一]s/(t)= === 【查看更多】

     

    题目列表(包括答案和解析)

    若方程ax2+bx+c=0的两实根为x1、x2,集合S={x|x＞x1},T={x|x＞x2},P={x|x＜x1},Q={x|x＜x2},则不等式ax2+bx+c＞0(a＞0)的解集为(    )

    A.(S∩T)∪(P∩Q)                               B.(S∩T)∩(P∩Q)

    C.(S∪T)∪(P∪Q)                               D.(S∪T)∩(P∪Q)

    查看答案和解析>>

    解不等式：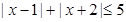

    【解析】本试题主要是考查了分段函数与绝对值不等式的综合运用。利用零点分段论 的思想，分为三种情况韬略得到解集即可。也可以利用分段函数图像来解得。

    解：方法一：零点分段讨论：   方法二：数形结合法：

     

    查看答案和解析>>

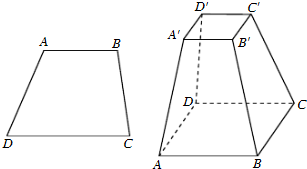    （必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
    方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
    设OE=x，∵△OAB∽△ODC，∴
    x
    x+h
    =
    a
    b
    ，即x=
    ah
    b-a
    ．
    ∴S梯形ABCD=S△ODC-S△OAB=
    1
    2
    b（x+h）-
    1
    2
    ax=
    1
    2
    （b-a）x+
    1
    2
    bh=
    1
    2
    （a+b）h．
    方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
    设梯形AMNB的高为x，MN=y，
    x
    h
    =
    y-a
    b-a
    ⇒y=a+
    b-a
    h
    x，∴S梯形ABCD=
    ∫
    h
    0
    （a+
    b-a
    h
    x）dx=（ax+
    b-a
    2h
    x2）
    |
    h
    0
    =ah+
    b-a
    2h
    •h2=
    1
    2
    （a+b）h．
    再解下面的问题：
    已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
    1
    3
    ×底面积×高）．

    查看答案和解析>>

    求圆心在直线y＝－2x上，并且经过点A(2,－1)，与直线x＋y＝1相切的圆的方程.

    【解析】利用圆心和半径表示圆的方程，首先

    设圆心为S，则KSA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3，  ………4分

    和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2)  

    ∴r＝＝,

    故所求圆的方程为：＋＝2

    解：法一：

    设圆心为S，则KSA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3，  ………4分

    和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2)             ……………………8分

    ∴r＝＝,                 ………………………10分

    故所求圆的方程为：＋＝2                   ………………………12分

    法二：由条件设所求圆的方程为：＋＝ 

     ,          ………………………6分

    解得a＝1,b＝－2, ＝2                     ………………………10分

    所求圆的方程为：＋＝2             ………………………12分

    其它方法相应给分

     

    查看答案和解析>>

    一直线运动的物体，从时间t到t+△t时，物体的位移为△s，那么
    lim
    △t→0
    △s
    △t
    为（　　）
    A、从时间t到t+△t时，物体的平均速度
    B、时间t时该物体的瞬时速度
    C、当时间为△t时该物体的速度
    D、从时间t到t+△t时位移的平均变化率

    查看答案和解析>>


    同步练习册答案