若已知二次函数y=f(x)的图象过原点，且1≤f(-1)≤2,3≤f(1)≤4.求f(-2)的范围.

已知二次函数y=f(x)的图象经过原点且1≤f(-1)≤2,3≤f(1)≤4,求f(-2)的范围.

若二次函数y=f(x)的图象过原点,且1≤f(-1)≤2,3≤f(1)≤4,求f(2)的取值范围.

   

 （满分１５分）定义在R上的函数f(x)=ax³+bx²+cx+d满足：函数f(x)的图象关于原点对称；函数f(x)的图象过点（3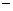，6）；函数f(x)在点x₁，x₂处取得极值，且|x₁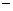x₂|=4．

（1）求f(x)表达式；

（2）求函数f(x)在点P（3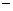，6）处切线方程；

（3）若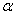、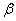∈R，求证：．

 

 

 

 

 

 

 

 

 

 

 

 

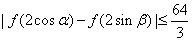若二次函数y=f(x)的图象经过原点，且1≤f(-1)≤2，3≤f(1)≤4，求f(-2)的范围．

分析：要求f(-2)的取值范围，只需找到含人f(-2)的不等式(组)．由于y=f(x)是二次函数，所以应先将f(x)的表达形式写出来．即可求得f(-2)的表达式，然后依题设条件列出含有f(-2)的不等式(组)，即可求解．