练习册

  • 练习册
  • 试题
    此时方程为x2+2x=3.它的根为x1=-3.x2=1．----------5分 【查看更多】

     

    题目列表(包括答案和解析)

    我们已学会了用“两边夹”的方法，根据不同的精确度要求，估算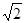的取值范围，我们还可以用“逼近”的方法，求出它的近似值．

    x
    		1.40
    		1.41
    		1.42
    		1.43
    		…
    x2
    		1.96
    		1.9881
    		2.0164
    		2.0449
    		…
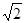    2－1.9881=0.0119，2.0164－2=0.0164，0.0119<0.0164
    可见1.9881比2.0164更逼近2，当精确度为0.01时，的近似值为1.41．
    下面，我们用同样的方法估计方程x2+2x=6其中一个解的近似值．
    x
    		1.63
    		1.64
    		1.65
    		1.66
    		…
    x2+2x
    		5.9169
    		5.9696
    		6.0225
    		6.0756
    		…
    根据上表，方程x2+2x=6的一个解约是______________．（精确到0.01）

    查看答案和解析>>

    以x为自变量的二次函数y=-x2+2x+m，它的图象与y轴交于点C（0，3），与x轴交于点A、B，精英家教网点A在点B的左边，点O为坐标原点，
    （1）求这个二次函数的解析式及点A，点B的坐标，画出二次函数的图象；
    （2）在x轴上是否存在点Q，在位于x轴上方部分的抛物线上是否存在点P，使得以A，P，Q三点为顶点的三角形与△AOC相似（不包含全等）？若存在，请求出点P，点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    先阅读下列解题过程，然后解答问题（1）、（2）、（3）．
    例：解绝对值方程：|2x|=1．
    解：讨论：①当x≥0时，原方程可化为2x=1，它的解是x=
    1
    2
    ．
    ②当x＜0时，原方程可化为-2x=1，它的解是x=-
    1
    2
    ．
    ∴原方程的解为x=
    1
    2
    和-
    1
    2
    ．
    问题（1）：依例题的解法，方程|
    1
    2
    x|    =3的解是
    x=6和-6
    x=6和-6
    ；
    问题（2）：尝试解绝对值方程：2|x-2|=6；
    问题（3）：在理解绝对值方程解法的基础上，解方程：|x-2|+|x-1|=3．

    查看答案和解析>>

    （2002•浙江）以x为自变量的二次函数y=-x2+2x+m，它的图象与y轴交于点C（0，3），与x轴交于点A、B，点A在点B的左边，点O为坐标原点，
    （1）求这个二次函数的解析式及点A，点B的坐标，画出二次函数的图象；
    （2）在x轴上是否存在点Q，在位于x轴上方部分的抛物线上是否存在点P，使得以A，P，Q三点为顶点的三角形与△AOC相似（不包含全等）？若存在，请求出点P，点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    以x为自变量的二次函数y=-x2+2x+m，它的图象与y轴交于点C（0，3），与x轴交于点A、B，点A在点B的左边，点O为坐标原点，
    （1）求这个二次函数的解析式及点A，点B的坐标，画出二次函数的图象；
    （2）在x轴上是否存在点Q，在位于x轴上方部分的抛物线上是否存在点P，使得以A，P，Q三点为顶点的三角形与△AOC相似（不包含全等）？若存在，请求出点P，点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>


    同步练习册答案