
题目列表(包括答案和解析)
 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).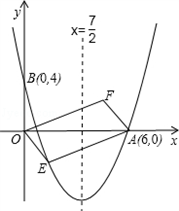
 的抛物线经过点A(6,0)和B(0,4)。
的抛物线经过点A(6,0)和B(0,4)。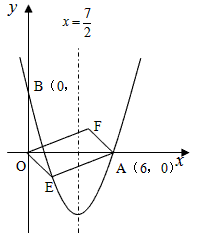
解:(1)A(-1,0),B(3,0),C(0,3).·················· 2分
抛物线的对称轴是:x=1.······················· 3分
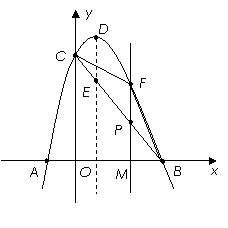 (2)①设直线BC的函数关系式为:y=kx+b.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
![]() 解得:k= -1,b=3.
解得:k= -1,b=3.
所以直线BC的函数关系式为:![]() .
.
当x=1时,y= -1+3=2,∴E(1,2).
当![]() 时,
时,![]() ,
,
∴P(m,![]() m+3).·························· 4分
m+3).·························· 4分
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]() ∴
∴![]() ········· 5分
········· 5分
∴线段DE=4-2=2,线段![]() ···· 6分
···· 6分
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
由![]() 解得:
解得:![]() (不合题意,舍去).
(不合题意,舍去).
因此,当![]() 时,四边形
时,四边形![]() 为平行四边形.··········· 7分
为平行四边形.··········· 7分
②设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,由
,由![]() 可得:
可得:![]()
∵![]() ························ 8分
························ 8分
即![]() .
.
![]()
![]() ·········· 9分
·········· 9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com