
题目列表(包括答案和解析)
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
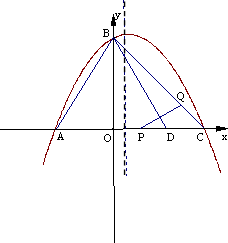
(1)求抛物线的解析式.
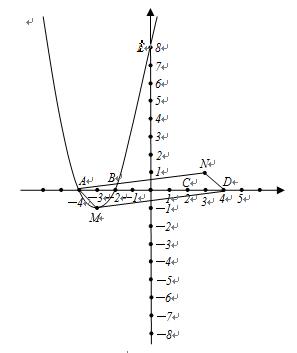
(2)已知AD=AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的条件下,M为抛物线的对称轴上一动点,当MQ+MC的值最小时,请求出点M的坐标.
知识迁移
当a>0且x>0时,因为(![]() )2≥0,所以x-2
)2≥0,所以x-2![]() +
+![]() ≥0,从而x+
≥0,从而x+![]() ≥2
≥2![]() (当x=
(当x=![]() 时取等号).
时取等号).
记函数y=x+![]() (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=![]() 时,该函数有最小值为2
时,该函数有最小值为2![]() .
.
直接应用
已知函数y1=x(x>0)与函数y2=![]() (x>0),则当x=________时,y1+y2取得最小值为________.
(x>0),则当x=________时,y1+y2取得最小值为________.
变形应用
已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求![]() 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
实际应用
已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共360元;二是燃油费,每千米为1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低是多少元?
设二次函数y=(a+b)x2+2cx-(a-b),其中a,b,c分别为△ABC的三边.
(1)当这个二次函数的图象与x轴只有一个交点时,试判断△ABC的形状;
(2)当x=-![]() 时,二次函数的最小值为-
时,二次函数的最小值为-![]() ,试判断△ABC的形状.
,试判断△ABC的形状.
作出二次函数y=-![]() x2-3x-
x2-3x-![]() 的草图.x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?函数y有最大值还是最小值?最值是多少?当x分别取何值时,y>0,y=0,y<0?
的草图.x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?函数y有最大值还是最小值?最值是多少?当x分别取何值时,y>0,y=0,y<0?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com