
题目列表(包括答案和解析)
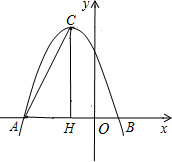 ,过顶点C作CH⊥x轴于点H.
,过顶点C作CH⊥x轴于点H.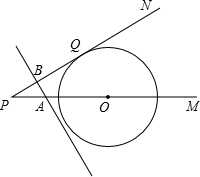 结果保留根号)
结果保留根号) 点P、Q.
点P、Q.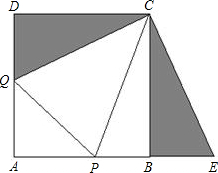 如图,正方形ABCD(四个角都是直角,四条边都相等)的边长为1,AB,AD上各有一点P、Q,△APQ的周长为2,求∠PCQ.为了解决这个问题,我们在正方形外以BC和AB的延长线为边作△CBE,使得△CBE≌△CDQ.
如图,正方形ABCD(四个角都是直角,四条边都相等)的边长为1,AB,AD上各有一点P、Q,△APQ的周长为2,求∠PCQ.为了解决这个问题,我们在正方形外以BC和AB的延长线为边作△CBE,使得△CBE≌△CDQ.| 1 | ||
|
| 1 |
| x-1 |
| 1 |
| 3 |
| p+q |
| 2 |
| pq |
| 1 |
| 10 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 15 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com