
题目列表(包括答案和解析)
(本小题满分12分)正在执行护航任务的某导弹护卫舰,突然收到一艘商船的求救信号,紧急前往相关海域.如图所示,到达相关海域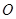 处后发现,在南偏西
处后发现,在南偏西 、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东
、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东 的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东
的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东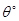 的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出
的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出 的值;如果未能追上,请说明理由.
的值;如果未能追上,请说明理由.

(本小题满分12分)正在执行护航任务的某导弹护卫舰,突然收到一艘商船的求救信号,紧急前往相关海域.如图所示,到达相关海域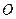 处后发现,在南偏西
处后发现,在南偏西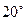 、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东
、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东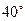 的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东
的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东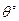 的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出
的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出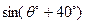 的值;如果未能追上,请说明理由.
的值;如果未能追上,请说明理由.
 处后发现,在南偏西
处后发现,在南偏西 、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东
、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东 的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东
的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东 的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出
的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出 的值;如果未能追上,请说明理由.
的值;如果未能追上,请说明理由.
已知递增等差数列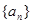 满足:
满足: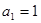 ,且
,且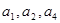 成等比数列.
成等比数列.
(1)求数列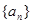 的通项公式
的通项公式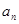 ;
;
(2)若不等式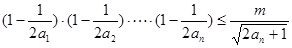 对任意
对任意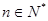 恒成立,试猜想出实数
恒成立,试猜想出实数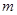 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列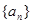 公差为
公差为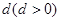 ,
,
由题意可知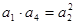 ,即
,即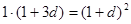 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于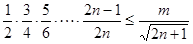 ,利用当
,利用当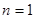 时,
时,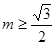 ;当
;当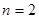 时,
时,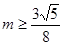 ;而
;而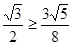 ,所以猜想,
,所以猜想,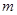 的最小值为
的最小值为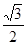 然后加以证明即可。
然后加以证明即可。
解:(1)设数列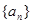 公差为
公差为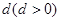 ,由题意可知
,由题意可知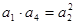 ,即
,即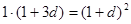 ,
,
解得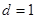 或
或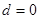 (舍去). …………3分
(舍去). …………3分
所以,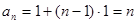 . …………6分
. …………6分
(2)不等式等价于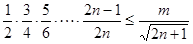 ,
,
当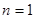 时,
时,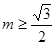 ;当
;当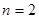 时,
时,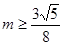 ;
;
而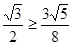 ,所以猜想,
,所以猜想,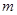 的最小值为
的最小值为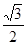 . …………8分
. …………8分
下证不等式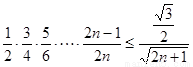 对任意
对任意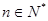 恒成立.
恒成立.
方法一:数学归纳法.
当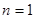 时,
时,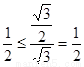 ,成立.
,成立.
假设当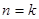 时,不等式
时,不等式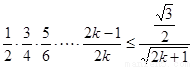 成立,
成立,
当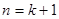 时,
时,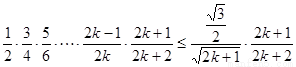 ,
…………10分
,
…………10分
只要证 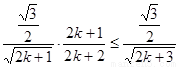 ,只要证
,只要证 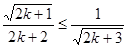 ,
,
只要证 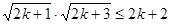 ,只要证
,只要证 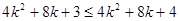 ,
,
只要证 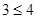 ,显然成立.所以,对任意
,显然成立.所以,对任意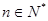 ,不等式
,不等式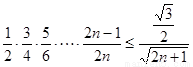 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 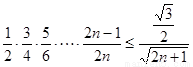
只要证 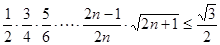 ,
,
设数列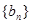 的通项公式
的通项公式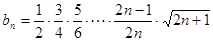 , …………10分
, …………10分
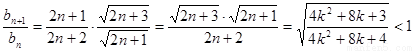 , …………12分
, …………12分
所以对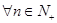 ,都有
,都有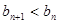 ,可知数列
,可知数列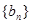 为单调递减数列.
为单调递减数列.
而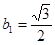 ,所以
,所以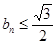 恒成立,
恒成立,
故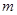 的最小值为
的最小值为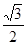 .
.
已知函数 ,
, 是
是 的一个零点,又
的一个零点,又 在
在 处有极值,在区间
处有极值,在区间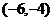 和
和 上是单调的,且在这两个区间上的单调性相反.(1)求
上是单调的,且在这两个区间上的单调性相反.(1)求 的取值范围;(2)当
的取值范围;(2)当 时,求使
时,求使 成立的实数
成立的实数 的取值范围.
的取值范围.
从而 或
或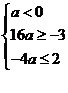 即
即 或
或
所以存在实数 ,满足题目要求.……………………12分
,满足题目要求.……………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com