
题目列表(包括答案和解析)
(本题满分12分)
为考察某种甲型H1N1疫苗的效果,进行动物实验,得到如下疫苗效果的实验列联表:
|
|
感染 |
未感染 |
总计 |
|
没服用 |
20 |
30 |
50 |
|
服用 |
x |
y |
50 |
|
总计 |
M |
N |
100 |
设从没服用疫苗的动物中任取两只,感染数为 从服从过疫苗的动物中任取两只,感染数为
从服从过疫苗的动物中任取两只,感染数为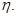 工作人员曾计算过
工作人员曾计算过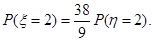
(1)求出列联表中数据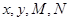 的值;
的值;
(2)写出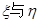 的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
的均值(不要求计算过程),并比较大小,请解释所得出的结论的实际意义;
(3)能够以97.5%的把握认为这种甲型H1N1疫苗有效么?并说明理由。
参考公式: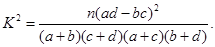
参考数据:
|
|
0.05 |
0.025 |
0.010 |
|
|
3.841 |
5.024 |
6.635 |
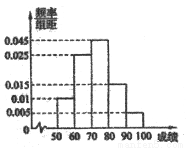
山东省《体育高考方案》于2012年2月份公布,方案要求以学校为单位进行体育测试,某校对高三1班同学按照高考测试项目按百分制进行了预备测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
(Ⅰ)请估计一下这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成一个小组.若选出的两人成绩差大于20,则称这两人为“帮扶组”,试求选出的两人为“帮扶组”的概率.
【解析】本试题主要考查了概率的运算和统计图的运用。
(1)由由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05,然后利用平均值公式,可知这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)
(2)中利用90~100分数段的人数为2人,频率为0.05;得到总参赛人数为40,然后得到0~60分数段的人数为40×0.1=4人,第五组中有2人,这样可以得到基本事件空间为15种,然后利用其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种,得到概率值
解:(Ⅰ)由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05; ……………2分
∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)…4分
(Ⅱ)∵90~100分数段的人数为2人,频率为0.05;
∴参加测试的总人数为 =40人,……………………………………5分
=40人,……………………………………5分
∴50~60分数段的人数为40×0.1=4人, …………………………6分
设第一组50~60分数段的同学为A1,A2,A3,A4;第五组90~100分数段的同学为B1,B2
则从中选出两人的选法有:(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种;其中两人成绩差大于20的选法有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2)共8种 …………………………11分
则选出的两人为“帮扶组”的概率为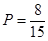
在 中,
中, 是三角形的三内角,
是三角形的三内角,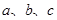 是三内角对应的三边,已知
是三内角对应的三边,已知 成等差数列,
成等差数列,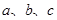 成等比数列
成等比数列
(Ⅰ)求角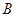 的大小;
的大小;
(Ⅱ)若 ,求
,求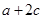 的值.
的值.
【解析】第一问中利用依题意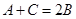 且
且 ,故
,故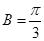
第二问中,由题意 又由余弦定理知
又由余弦定理知
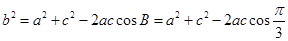
,得到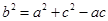 ,所以
,所以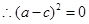 ,从而得到结论。
,从而得到结论。
(1)依题意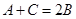 且
且 ,故
,故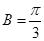 ……………………6分
……………………6分
(2)由题意 又由余弦定理知
又由余弦定理知
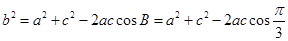 …………………………9分
…………………………9分
即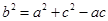 故
故
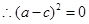
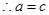 代入
代入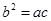 得
得

已知递增等差数列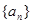 满足:
满足: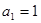 ,且
,且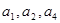 成等比数列.
成等比数列.
(1)求数列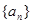 的通项公式
的通项公式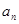 ;
;
(2)若不等式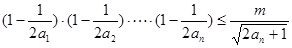 对任意
对任意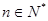 恒成立,试猜想出实数
恒成立,试猜想出实数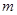 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列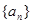 公差为
公差为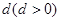 ,
,
由题意可知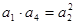 ,即
,即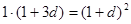 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于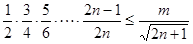 ,利用当
,利用当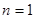 时,
时,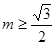 ;当
;当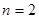 时,
时,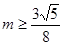 ;而
;而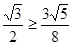 ,所以猜想,
,所以猜想,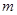 的最小值为
的最小值为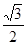 然后加以证明即可。
然后加以证明即可。
解:(1)设数列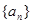 公差为
公差为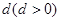 ,由题意可知
,由题意可知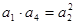 ,即
,即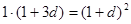 ,
,
解得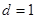 或
或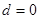 (舍去). …………3分
(舍去). …………3分
所以,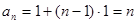 . …………6分
. …………6分
(2)不等式等价于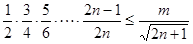 ,
,
当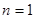 时,
时,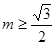 ;当
;当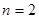 时,
时,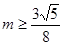 ;
;
而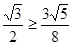 ,所以猜想,
,所以猜想,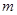 的最小值为
的最小值为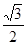 . …………8分
. …………8分
下证不等式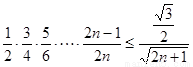 对任意
对任意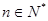 恒成立.
恒成立.
方法一:数学归纳法.
当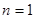 时,
时,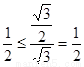 ,成立.
,成立.
假设当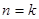 时,不等式
时,不等式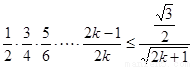 成立,
成立,
当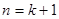 时,
时,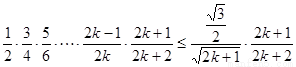 ,
…………10分
,
…………10分
只要证 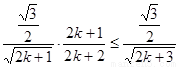 ,只要证
,只要证 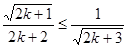 ,
,
只要证 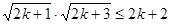 ,只要证
,只要证 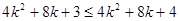 ,
,
只要证 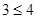 ,显然成立.所以,对任意
,显然成立.所以,对任意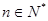 ,不等式
,不等式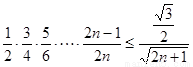 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 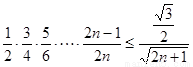
只要证 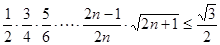 ,
,
设数列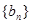 的通项公式
的通项公式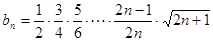 , …………10分
, …………10分
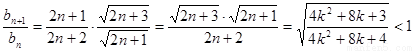 , …………12分
, …………12分
所以对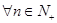 ,都有
,都有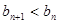 ,可知数列
,可知数列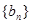 为单调递减数列.
为单调递减数列.
而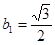 ,所以
,所以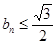 恒成立,
恒成立,
故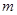 的最小值为
的最小值为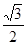 .
.
已知幂函数 满足
满足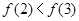 。
。
(1)求实数k的值,并写出相应的函数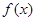 的解析式;
的解析式;
(2)对于(1)中的函数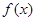 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数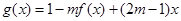 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数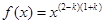 满足
满足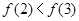 ,得到
,得到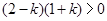
因为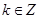 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为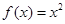
(2)由(1)知,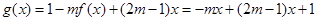 ,
,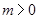 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: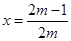 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到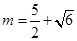
(1)对于幂函数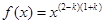 满足
满足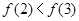 ,
,
因此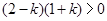 ,解得
,解得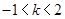 ,………………3分
,………………3分
因为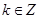 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时,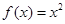 ,
,
当k=1时,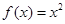 ,综上所述,k的值为0或1,
,综上所述,k的值为0或1,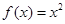 。………………6分
。………………6分
(2)函数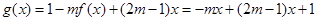 ,………………7分
,………………7分
由此要求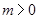 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: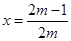 ,
,
当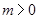 时,
时,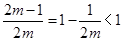 ,因为在区间
,因为在区间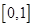 上的最大值为5,
上的最大值为5,
所以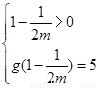 ,或
,或 …………………………………………10分
…………………………………………10分
解得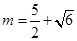 满足题意
满足题意
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com