
题目列表(包括答案和解析)
已知数列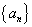 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
(1)求证:{ }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
19.已知数列![]() ,首项a 1 =3且2a n+1=S n ?S n-1 (n≥2).
,首项a 1 =3且2a n+1=S n ?S n-1 (n≥2).
(1)求证:{![]() }是等差数列,并求公差;
}是等差数列,并求公差;
(2)求{a n }的通项公式;
(3)数列{an }中是否存在自然数k0,使得当自然数k≥k 0时使不等式a k>a k+1对任意大于等于k的自然数都成立,若存在求出最小的k值,否则请说明理由.
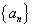 ,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).
,首项a 1 =3且2a n+1="S" n?S n-1 (n≥2).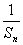 }是等差数列,并求公差;
}是等差数列,并求公差;已知向量m=(a,-x),n=(ln(1+ex),a+1),![]() = m?n,
= m?n,![]()
且![]() 在x=1处取得极值.
在x=1处取得极值.
(1)求a的值,并判断![]() 的单调性;
的单调性;
(2)当![]() ;
;
(3)设△ABC的三个顶点A、B、C都在![]() 图像上,横坐标依次成等差数列,证明:△ABC为钝角三角形,并判断是否可能是等腰三角形,说明理由.
图像上,横坐标依次成等差数列,证明:△ABC为钝角三角形,并判断是否可能是等腰三角形,说明理由.
已知![]() (m为常数,m>0且
(m为常数,m>0且![]() ),设
),设![]() 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(Ⅰ)求证:数列{an}是等比数列;
(Ⅱ)若bn=an?![]() ,且数列{bn}的前n项和Sn,当
,且数列{bn}的前n项和Sn,当![]() 时,求Sn;
时,求Sn;
(Ⅲ)若cn=![]() ,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,说明理由.
,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com