
题目列表(包括答案和解析)
| Mm |
| r |
| 1 |
| 2 |
理论证明,取离星球中心无穷远处为引力势能的零势点时,则物体在距离星球中心为r处的引力势能可表示为:![]() .www.ks5u.comG为万有引力常数,M、m表示星球与物体的质量,而万有引力做的功则为引力势能减少.已知月球质量为M、半径为R,探月飞船的总质量为m,月球表面的重力加速度为g,万有引力常数G.
.www.ks5u.comG为万有引力常数,M、m表示星球与物体的质量,而万有引力做的功则为引力势能减少.已知月球质量为M、半径为R,探月飞船的总质量为m,月球表面的重力加速度为g,万有引力常数G.
求飞船在距月球表面H(H>R/3)高的环月轨道运行时的速度;www.ks5u.com
设将飞船从月球表面发送到上述环月轨道的能量至少为E.有同学提出了一种计算此能量E的方法:根据![]() ,将(1)中的
,将(1)中的![]() 代入即可.请判断此方法是否正确,并说明理由,如不正确,请给出正确的解法与结果.(不计飞船质量的变化及其他天体的引力和月球的自转)
代入即可.请判断此方法是否正确,并说明理由,如不正确,请给出正确的解法与结果.(不计飞船质量的变化及其他天体的引力和月球的自转)
| Mm |
| r |
| R |
| 3 |
| 1 |
| 2 |
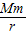 ,式中G为万有引力常数,M、m表示星球与物体的质量,而万有引力做的正功等于引力势能的减少.已知月球质量为M、半径为R,探月飞船的总质量为m.月球表面的重力加速度为g.
,式中G为万有引力常数,M、m表示星球与物体的质量,而万有引力做的正功等于引力势能的减少.已知月球质量为M、半径为R,探月飞船的总质量为m.月球表面的重力加速度为g.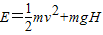 ,将(1)中的v代入即可.请判断此方法是否正确,并说明理由.如不正确,请给出正确的解法与结果(不计飞船质量的变化及其他天体的引力).
,将(1)中的v代入即可.请判断此方法是否正确,并说明理由.如不正确,请给出正确的解法与结果(不计飞船质量的变化及其他天体的引力). .G为万有引力常数,M、m表示星球与物体的质量,而万有引力做的功则为引力势能的减少.已知月球质量为M、半径为R,探月飞船的总质量为m.月球表面的重力加速度为g,万有引力常数G.
.G为万有引力常数,M、m表示星球与物体的质量,而万有引力做的功则为引力势能的减少.已知月球质量为M、半径为R,探月飞船的总质量为m.月球表面的重力加速度为g,万有引力常数G. )高的环月轨道运行时的速度v;
)高的环月轨道运行时的速度v; ,将(1)中的v代入即可.请判断此方法是否正确,并说明理由.如不正确,请给出正确的解法与结果(不计飞船质量的变化及其他天体的引力和月球的自转).
,将(1)中的v代入即可.请判断此方法是否正确,并说明理由.如不正确,请给出正确的解法与结果(不计飞船质量的变化及其他天体的引力和月球的自转).
1-5.CACDD
6-9.ABC BD BD ACD
10.(1)匀速直线运动(2分), A球(平抛运动小球)水平方向的分运动是匀速直线运动(4分) (2) m/s(4分)
m/s(4分)
11.(1)0.2,5
(每空2分,共4分)
(2)图略(水滴应出现在5、20、45、80、125、
12.(1) 220, 先接通电源后释放纸带 (每空1分,共2分)
(2) S1、 S6; S1、S2、S3、S4、S5、S6; B; 偶然。(每空1分,共4分)
(3) 重物下落过程中受到阻力; S1、S2、S3、S4、S5、S6 长度测量;
交流电频率波动; 数据处理方法等。(每答对1条得2分,共4分)
13.(12分)解析:设物体与水平面的动摩擦因数为μ,B从断线到停止运动前进s2,A从断线到停止运动前进s1.
对B列动能定理方程,有 -μ mgs2=- mv2 ……………(1)(3分)
mv2 ……………(1)(3分)
对A列动能定理方程,有 Fs0-μ?2mgs1=- mv2……………(2)(3分)
mv2……………(2)(3分)
断线前,系统处于平衡状态,有 F=μ?3mg……………(3)(2分)
由上述三个方程可得 s1-s2= s0……………(4)(2分)
s0……………(4)(2分)
则A、B两物相距 Δs=L+s1-s2=L+ s0……………(5)(2分)
s0……………(5)(2分)
14.(15分)解析:(1)探月飞船作圆周运动所需的向心力由月球对探月飞船的万有引力提供有  ……………(1) (3分)
……………(1) (3分)
 ……………(2) (2分)
……………(2) (2分)
(2)不正确 ; 因探月飞船从月球表面发送到H高处的过程中月球的引力为变力,故克服引力所做的功不等于mgH. ……………(3)(2分)
由引力势能定义可知探月飞船从月球表面发送到H处引力势能的改变量
 ……………(4)(2分)
……………(4)(2分)
整理后得  ……………(5)(2分)
……………(5)(2分)
由能量守恒定律可知,将探月飞船从月球表面发送到H处所需的能量为
 ……………(6)(2分)
……………(6)(2分)
联立求解得  ……………(7)(2分)
……………(7)(2分)
15.(16分)
(1)a1= = m/s2=
v1= a1?Δt1=0.2×
(2)x2=a1Δt12+ v1Δt2=×0.2×
 y2= a2Δt22 =×0.2×
y2= a2Δt22 =×0.2×
 (3)v22=2 v12, v 2=v1=×
(3)v22=2 v12, v 2=v1=×
a3== m/s2=
m/s2=
 E3= =
E3= = =1.4×106V/m (2分)
=1.4×106V/m (2分)
 (4)如图
(2分)
(4)如图
(2分)
16.(16分)(1)设轨道半径为R,由机械能守恒定律;
 ……………(1)(2分)
……………(1)(2分)
对B点: ………(2)(2分)
………(2)(2分)
对A点: ……(3)(2分)
……(3)(2分)
由(1)(2)(3)式得:
两点压力差  ………(4)(2分)
………(4)(2分)
由图象得:截距 得
得 ………(5)(2分)
………(5)(2分)
(2)因为图线的斜率 得
得 ……(6)(2分)
……(6)(2分)
在A点不脱离的条件为: ……(7)(2分)
……(7)(2分)
由(1)(5)(6)(7)式得: ………(8)(2分
………(8)(2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com