
题目列表(包括答案和解析)
复数 =
=
A. ; B.
; B.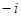 ; C.
; C. ; D.
; D.
化简
A. ; B.
; B. ; C.
; C.
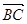 ; D.
; D.  ;
;
复数 =
=
A. ; ; | B. ; ; | C. ; ; | D. |
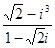 =
=A. ; ; | B. ; ; | C. ; ; | D. |

A. ; ; | B.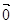 ; ; | C. ; ; | D. ; ; |
一、填空题:(5’×11=55’)
题号
1
2
3
4
5
6
答案
.files/image190.gif)
.files/image192.gif)
0
(1,2)
2
.files/image194.gif)
题号
7
8
9
10
11
答案
.files/image196.gif)
4
8.3
.files/image198.gif)
②、③
二、选择题:(4’×4=16’)
题号
12
13
14
15
答案
A
C
B
|