
题目列表(包括答案和解析)
 四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=
四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=| π | 3 |
| 5 |
| 2 |
| 4 |
| 3 |
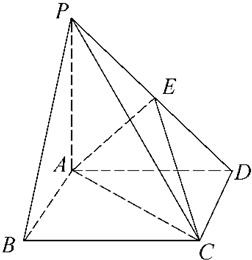
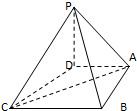 在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=AD=a,BC=2a,PD⊥底面ABCD,PD=3a.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=AD=a,BC=2a,PD⊥底面ABCD,PD=3a.| PF | FD |
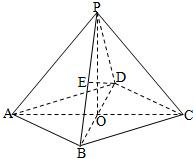 在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°.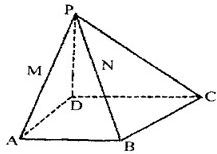 在四棱锥P-ABCD中,AB⊥AD,CD∥AB,PD⊥底面ABCD,AB=
在四棱锥P-ABCD中,AB⊥AD,CD∥AB,PD⊥底面ABCD,AB=| 2 |
一、填空题:(5’×11=55’)
题号
1
2
3
4
5
6
答案
.files/image190.gif)
.files/image192.gif)
0
(1,2)
2
.files/image194.gif)
题号
7
8
9
10
11
答案
.files/image196.gif)
4
8.3
.files/image198.gif)
②、③
二、选择题:(4’×4=16’)
题号
12
13
14
15
答案
A
C
B
|