
题目列表(包括答案和解析)
(本题满分16分,第1小题6分,第2小题10分)
已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,若椭圆
的左、右焦点,若椭圆![]() 的焦距为2.
的焦距为2.
⑴求椭圆![]() 的方程;
的方程;
⑵设![]() 为椭圆上任意一点,以
为椭圆上任意一点,以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当圆
,当圆![]() 与椭圆的右准线
与椭圆的右准线 ![]() 有公共点时,求△
有公共点时,求△![]() 面积的最大值.
面积的最大值.
(本题满分16分,第1小题6分,第2小题10分)
已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,若椭圆
的左、右焦点,若椭圆![]() 的焦距为2.
的焦距为2.
⑴求椭圆![]() 的方程;
的方程;
⑵设![]() 为椭圆上任意一点,以
为椭圆上任意一点,以![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当圆
,当圆![]() 与椭圆的右准线
与椭圆的右准线 ![]() 有公共点时,求△
有公共点时,求△![]() 面积的最大值.
面积的最大值.
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
 (本题满分16分,第(1)小题6分,第(2)小题10分)
(本题满分16分,第(1)小题6分,第(2)小题10分)
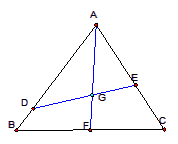
如图,已知点![]() 是边长为
是边长为![]() 的正三角形
的正三角形![]() 的中心,线段
的中心,线段![]() 经过点
经过点![]() ,并绕点
,并绕点![]() 转动,分别交边
转动,分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ;设
;设![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(1)求表达式![]() 的值,并说明理由;
的值,并说明理由;
(2)求![]() 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的![]() 、
、![]() 的值.
的值.
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
一、填空题:(5’×11=55’)
题号
1
2
3
4
5
6
答案
.files/image190.gif)
.files/image192.gif)
0
(1,2)
2
.files/image194.gif)
题号
7
8
9
10
11
答案
.files/image196.gif)
4
8.3
.files/image198.gif)
②、③
二、选择题:(4’×4=16’)
题号
12
13
14
15
答案
A
C
B
|