题目列表(包括答案和解析)
静电场与引力场有着非常相似的性质，力的形式都遵从平方反比定律，解答下列问题：静电场与引力场有着非常相似的性质，力的形式都遵从平方反比定律，解答下列问题：
（1）写出万有引力定律和库仑定律中的常数G与K的单位。
（2）某星球的质量为M，在该星球表面某一倾角为θ的山坡上以初速度v0平抛一个物体，经
时间该物体落到山坡上。欲使该物体不再落回该星球的表面，至少应以多大的速度抛出物体（不计一切阻力，万有引力常量为G）？
（3）如图所示，质量为m的小球A穿在绝缘细杆上，杆的倾角为α，小球A带正电，电量为q，在杆上B点处固定一个电量为Q的正电荷。将A由距B竖直高度为H处无初速释放，小球A下滑过程中电量不变。不计A与细杆间的摩擦，整个装置处在真空中。已知静电力恒量k和重力加速度g，求：A球刚释放时的加速度以及当A球的动能最大时，A球与B点的距离。
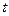时间该物体落到山坡上。欲使该物体不再落回该星球的表面，至少应以多大的速度抛出物体（不计一切阻力，万有引力常量为G）？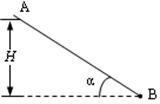
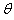的山坡上以初速度v0平抛一个物体，经t时间该物体落到山坡上。欲使该物体不落在该星球的表面，至少应以多大的速度抛出物体（不计一切阻力，万有引力常量为G）？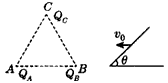 
1
2
3
4
5
6
7
8
9
10
11
12
B
AC
B
C
BCD
D
AC
D
BC
AC
BD
A
13．A组（1）球形体；（1分）V/S；（1分）10-10，（1分）3.0×10-29（2分）
（2）增大，（2分）变多，（2分）??273.15（1分）
B组(1)x轴正方向，（1分）a，（1分）c，（1分）；100（2分）
（2）小于（2分）大于 （2分） Υ1<Υ2<Υ3（1分）
14．（1）步骤C不必要, （2分） 步骤B是错误的．（2分）
（2）（4分）
（3）重锤的质量m ，（1分）
（3分）
15．（1）3.550×10-3 （3分） （2）πd2Rx/
（3）将电键S2接1，只调节滑动变阻器r，使电压表读数尽量接近满量程，读出这时电压表和电流表的示数U2、I2 （2分） U1/I1－U2/I2（3分）
提示：由欧姆定律得U1=I1(RA+RP+Rx)，U2=I2(RA+RP)，故Rx=U1/I1－U2/I2.
16．（1）N?m2/kg2 （2分） N?m2?C-2（2分）
（2）解析：由题意可知是要求该星球上的“近地卫星”的绕行速度，也即为第一宇宙速度。设该星球表面处的重力加速度为
，由平抛运动可得
① 故
2分
对于该星球表面上的物体有
②所以
2分
而对于绕该星球做匀速圆周运动的“近地卫星”应有
③ 2分
由 ①②③式得 
④ 1分
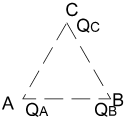
（3）受力情况如图所示，QA、QB对QC的作用力大小和方向都不因其它电荷的存在而改变，仍然遵守库仑定律的规律。
QA对QC作用力：
，同性电荷相斥。（1分）
QB对QC作用力：
，异性电荷相吸。（1分）
∵QA=QB=Q ∴FA=FB
根据平行四边形法则，QC受的力F1即为FA、FB的合力，根据几何知识可知，QC受力的大小，F1=FA=FB=
=
，（3分）
方向为平行AB连线向右。（2分）
17．（16分）解：(1)ab杆向右运动时，ab杆中产生的感应电动势方向为a→b，大小为E=BLv1（1分）
cd杆中的感应电流方向为d→c. cd杆受到的安培力方向水平向右 （1分）
安培力大小为
（2分）
cd杆向下匀速运动，有mg=μF安 ② （1分）
解①、②两式，ab杆匀速运动的速度为
（2分）
（2）ab杆所受拉力
（4分）
（3）设cd杆以v2速度向下运动h过程中，ab杆匀速运动了s距离
（2分）
整个回路中产生的焦耳热等于克服安培力所做的功
（3分）
18．．解：（17分）(1)带电微粒在做匀速圆周运动，电场力与重力应平衡，有mg=Eq，即E= mg/q，（3分）方向竖直向下． （1分）
(2) 粒子做匀速圆周运动，轨道半径为R，如图所示。
， （1分）
最高点与地面的距离为
，（1分）
解得
。（2分） 该微粒运动周期为T=
,（1分）
运动至。最高点所用时间为
.（2分）
(3)设粒子上升高度为h，由动能定理得
，（3分）
解得
。 （2分） 微粒离地面最大高度为H+
。（1分）
19（17分）解析：（1）解除锁定弹开AB后，AB两物体的速度大小：
（2分）
弹簧储存的弹性势能
（1分）
（2）B滑上传送带匀减速运动，当速度减为零时，滑动的距离最远．
由动能定理得：
（2分） 得：
1分）
（3）物块B沿传送带向左返回时，先匀加速运动，物块速度与传送带速度相同时一起匀速运动，设物块B加速到传送带速度v需要滑动的距离为
由
得
（2分）
表明物块B滑回水平面MN的速度没有达到传送带速度
所以: 
（1分）
（4）设弹射装置对A做功为
，则：
（1分）
AB碰后速度互换，B的速度 
=
（1分）
B要刚好能滑出平台Q端，由能量关系有：
（1分）
又mA=mB， 联立解得：
（1分）
（1分）
B滑过传送带过程，传送带移动的距离：
（1分)
所求内能：
(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com