
题目列表(包括答案和解析)
如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连。质量为m、边长为l、电阻不计的正方形线框垂直于导轨并可在导轨上滑动。整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B。滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态。现若从静止开始释放物块,用h表示物块下落的高度(物块不会
触地),g表示重力加速度,其他电阻不计,则 ( )
A.因通过正方形线框的磁通量始终不变,故电阻R中没有感应电流
B.物体下落的加速度为0.5g
C.若h足够大,物体下落的最大速度为![]()
D.通过电阻R的电量为![]()

如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连。质量为m、边长为l、电阻不计的正方形线框垂直于导轨并可在导轨上滑动。整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B。滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态。现若从静止开始释放物块,用h表示物块下落的高度(物块不会触地),g表示重力加速度,其他电阻不计,则 ( )
A.因通过正方形线框的磁通量始终不变,故电阻R中没有感应电流
B.物体下落的加速度为0.5g
C.若h足够大,物体下落的最大速度为![]()
D.通过电阻R的电量为![]()
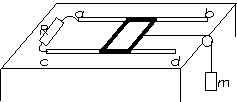
如图,在水平桌面上放置两条相距l的平行光滑导轨ab与cd,阻值为R的电阻与导轨的a、c端相连。质量为m、边长为l、电阻不计的正方形线框垂直于导轨并可在导轨上滑动。整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B。滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一个质量也为m的物块相连,绳处于拉直状态。现若从静止开始释放物块,用h表示物块下落的高度(物块不会触地),g表示重力加速度,其他电阻不计,则( )
A.因通过正方形线框的磁通量始终不变,故电阻R中没有感应电流
B.物体下落的加速度为0.5g
C.若h足够大,物体下落的最大速度为![]()
D.通过电阻R的电量为![]()

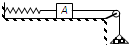 如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )
如图所示,木块A放在水平桌面上.木块左端用轻绳与轻质弹簧相连,弹簧的左端固定,用一轻绳跨过光滑定滑轮,一端连接木块右端,另一端连接一砝码盘(装有砝码),轻绳和弹簧都与水平桌面平行.当砝码和砝码盘的总质量为0.5kg时,整个装置静止,弹簧处于伸长状态,弹力大小为3N.若轻轻取走盘中的部分砝码,使砝码和砝码盘的总质量减小到0.1kg,取g=10m/s2,此时装置将会出现的情况是( )| A、弹簧伸长的长度减小 | B、桌面对木块的摩擦力大小不变 | C、木块向右移动 | D、木块所受合力将变大 |
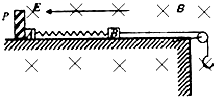 如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B连接,另一端连接轻质小钩.整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B、方向水平向里的匀强磁场中.物块A,B开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面.若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则
如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B连接,另一端连接轻质小钩.整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B、方向水平向里的匀强磁场中.物块A,B开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面.若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则一、选择题(48分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
AC
BC
D
ACD
BD
AD
AC
C
D
B
BD
二、非选择题
13.(4分)(1)1.997;1.094;
(2)(8分)30.7
14.(6分) (1)4.0 Ω (2) 3.0V 2.0Ω (每空2分)
15.(10分)(1)0.495~
(3) (2分)偏大(2分)
(2分)偏大(2分)
16.(16分)(1)设带电体在水平轨道上运动的加速度大小为a,根据牛顿第二定律有
qE=ma 解得:
a=qE/m=
设带电体运动到B端的速度大小为vB,则:
vB2=2as 解得:
vB= =
=
(2)设带电体运动到圆轨道B端时受轨道的支持力为N,根据牛顿第二定律有
N-mg=mvB2/R 解得: N=mg+ mvB2/R=5.0N……(3分)
根据牛顿第三定律可知,带电体对圆弧轨道B端的压力大小:N′=N=5.0N (1分)
(3)因电场力做功与路径无关,所以带电体沿圆弧形轨道运动过程中,电场力所做的功:
W电=qER=0.32J (3分)
设带电体沿圆弧形轨道运动过程中摩擦力所做的功为W摩,对此过程根据动能定理有
W电+W摩-mgR=0- mvB2
(3分)
mvB2
(3分)
解得: W摩=-0.72J (2分)
17.(20分)⑴ 从A点射出的粒子,由A到A′的运动时间为T,根据运动轨迹和对称性可得:
x轴方向  (3分)
(3分)
y轴方向 (3分)
(3分)
解得: (2分)
(2分)
⑵ 设到C点距离为△y处射出的粒子通过电场后也沿x轴正方向,粒子第一次达x轴用时△t,水平位移为△x,则

 (4分)
(4分)
粒子从电场射出时的速度方向也将沿x轴正方向,则
 (3分)
(3分)
解之得: (3分)
(3分)
即AC间y坐标为 (n = 1,2,3,……) (2分)
(n = 1,2,3,……) (2分)
18.(20分)(1)设物体B自由下落与物体A相碰时的速度为v0,则
 解得:v0=
解得:v0=
设A与B碰撞结束后的瞬间速度为v1,根据动量守恒定律
 解得:v1=
解得:v1=
(2)设物体A静止在弹簧上端时弹簧的压缩量为x1,  1分
1分
设弹簧劲度系数为k,根据胡克定律有
 解得:k=100N/m 3分
解得:k=100N/m 3分
两物体向上运动过程中,弹簧弹力等于两物体总重力时具有最大速度 1分
设此时弹簧的压缩量为x2,则
 解得:x2=
解得:x2=
设此时弹簧的长度为l,则
解得:l=
(3)两物体向上运动过程中在弹簧达到原长时分离, 从碰后到分离的过程,物体和弹簧组成的系统机械能守恒,因此有
 3分
3分
解得: 2分
2分
19.(20分)(1)设A、B的轨道半径分别为r1、r2,它们做圆周运动的周期T、角速度ω都相同,根据牛顿运动定律有  2分
2分
即 1分
1分
A、B之间的距离 1分
1分
根据万有引力定律 2分
2分
得 2分
2分
(2)对可见星A有 2分
2分
其中 1分
1分
得: 2分
2分
(3)设m2=nm(n>0),并根据已知条件m1=6ms,及相关数据代入上式得
 2分
2分
由数学知识知 在n>0是增函数
1分
在n>0是增函数
1分
当n=2时, 1分
1分
所以一定存在n>2,即m2>2ms,可以判断暗星B可能是黑洞 2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com